Question

【题目】如图，已知直线y＝x+b与y轴交于点B（0，﹣3），与反比例函数y＝（x＞0）的图象交于点A，与x轴交于点C，BC＝3AC

（1）求反比例函数的解析式；

（2）若P是y轴上一动点，M是直线AB上方的反比例函数y＝（x＞0）的图象上一动点，直线MN⊥x轴交直线AB于点N，求△PMN面积的最大值．

Answer 1

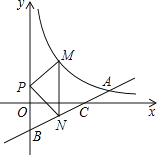
【答案】（1）反比例函数的解析式为y＝；（2）

【解析】

（1）易求得直线的解析式为y＝x﹣3，作AD⊥x轴于D，根据平行线分线段成比例定理求得AD＝1，在A的纵坐标为1，代入直线解析式求得横坐标，把A（8，1）代入y＝（x＞0）即可求得k的值；

（2）设M（x，），则N（x，x﹣3），得到MN＝﹣+3，根据三角形面积公式得到S△PMN＝﹣（x﹣3）2+，从而求得△PMN面积的最大值是．

解：（1）∵直线与y轴交于点B（0，﹣3），

∴b＝﹣3，

∴直线为y＝﹣3，

作AD⊥x轴于D，

∴AD∥OB，

∴

∵点B（0，﹣3），BC＝3AC，

∴，

∴AD＝1，

把y＝1代入y＝﹣3得，1＝﹣3，解得x＝8，

∴A（8，1），

∵反比例函数y＝（x＞0）的图象经过点A，

∴k＝8×1＝8，

∴反比例函数的解析式为y＝；

（2）设M（x，），则N（x，x﹣3），

∴MN＝﹣+3，

∴S△PMN＝，

∵﹣＜0，

∴△PMN面积的最大值是．