Question

【题目】四边形 ABCD 中，E 为边 BC 上一点，F 为边 CD 上一点，且∠AEF=90°．

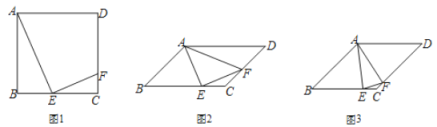
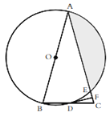
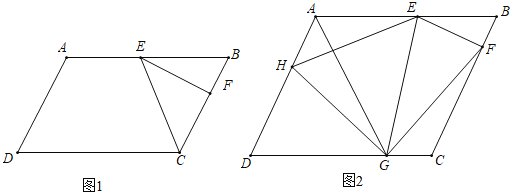
（1）如图 1，若 ABCD 为正方形，E 为 BC 中点，求证：．

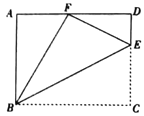
（2）若 ABCD 为平行四边形，∠AFE=∠ADC，

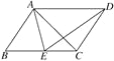
①如图 2，若∠AFE=60°，求的值；

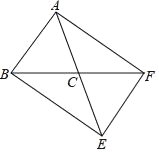
②如图 3，若 AB=BC，EC=2CF．直接写出 cos∠AFE 值为　　　．

Answer 1

【答案】（1）见解析（2）（3）

【解析】

（1）如图1中，设正方形的边长为2a．只要证明△ABE∽△ECF，可得，求出CF、DF即可解决问题；

（2）如图2中，在AD上取一点H，使得FH＝DF．只要证明△AEF是等边三角形，推出AF＝2EF，再证明△AHF∽△FCE，可得EC：HF＝EF：AF＝1：2;

（3）如图3，作FT＝FD交AD于点T，作FH⊥AD于H，证△FCE∽△ATF，设CF＝2，则CE＝4，可设AT＝x，则TF＝2x，AD＝CD＝2x＋2，DH＝DT＝，分别用含x的代数式表示出∠AFE和∠D的余弦值，列出方程，求出x的值，即可求出结论．

（1）证明：如图1中，设正方形的边长为2a．

∵四边形ABCD是正方形，

∴∠B＝∠C＝90°，

∵∠AEF＝90°，

∴∠AEB＋∠FEC＝90°，∠FEC＋∠EFC＝90°，

∴∠AEB＝∠EFC，

∴△ABE∽△ECF，

∴

∵BE＝EC＝a，AB＝CD＝2a，

∴CF＝a，DF＝CDCF＝a，

∴ ；

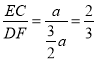（2）如图2中，在AD上取一点H，使得FH＝DF，

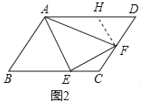
∵∠AEF＝90°，∠AFE＝∠D＝60°，

∴AF＝2EF，

∵FH＝DF，

∴△DHF是等边三角形，

∴∠FHD＝60°，

∴∠AHF＝120°，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠C＝180°∠D＝120°，

∴∠AHF＝∠C，

∵∠AFC＝∠D＋∠FAH＝∠EFC＋∠AFE，∠AFE＝∠D，

∴∠HAF＝∠EFC，

∴△AHF∽△FCE，

∴EC：HF＝EF：AF＝1：2，

∴；

如图3，作FT＝FD交AD于点T，作FH⊥AD于H，

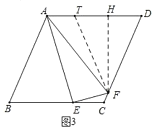
则∠FTD＝∠FDT，

∴180°∠FTD＝180°∠D，

∴∠ATF＝∠C，

又∵∠TAF＋∠D＝∠AFE＋∠CFE，且∠D＝∠AFE，

∴∠TAF＝∠CFE，

∴△FCE∽△ATF，

∴＝，

设CF＝2，则CE＝4，可设AT＝x，则TF＝2x，AD＝CD＝2x＋2，

∴DH＝DT＝，且，

由cos∠AFE＝cos∠D，得，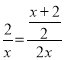

解得x＝6，（x=0舍去）

∴cos∠AFE＝＝．