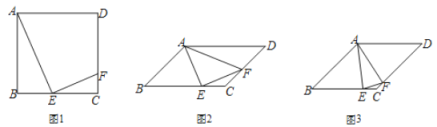
[题目]图1.图2分别是一滑雪运动员在滑雪过程中某一时刻的实物图与示意图.已知运动员的小腿与斜坡垂直.大腿与斜坡平行.且三点共线.若雪仗长为...求此刻运动员头部到斜坡的高度(精确到)(参考数据:) 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】图1，图2分别是一滑雪运动员在滑雪过程中某一时刻的实物图与示意图，已知运动员的小腿与斜坡垂直，大腿与斜坡平行，且三点共线，若雪仗长为，，，求此刻运动员头部到斜坡的高度（精确到）（参考数据：）

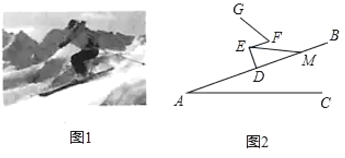
【答案】1.3m

【解析】

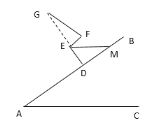
由三点共线，连接GE，根据ED⊥AB，EF∥AB，求出∠GEF=∠EDM=90°，利用锐角三角函数求出GE，根据直角三角形30°角所对的直角边等于斜边的一半求出DE，即可得到答案.

三点共线，连接GE，

∵ED⊥AB，EF∥AB，

∴∠GEF=∠EDM=90°，

在Rt△GEF中，∠GFE=62°，，

∴m，

在Rt△DEM中，∠EMD=30°，EM=1m，

∴ED=0.5m，

∴h=GE+ED=0.75+0.5m，

答：此刻运动员头部到斜坡的高度约为1.3m.

练习册系列答案

两次摸到相同颜色的球的概率；

在上面的问题中，如果从中随机摸出1个球，记下颜色后不放回，再从中随机摸出1个球，求两次摸到的球的颜色能配成紫色红色与蓝色配成紫色的概率．

【题目】小颖在完成一项“社会调查”作业时，需要调查城市送餐人员的收入情况，他了解到劳务公司为了鼓励送餐员的工作积极性，实行“月总收入基本工资（固定）送餐单数奖励”的方法计算薪资，调查中获得如下信息：

送餐员	小李	小杨
月送餐单数/单	292	273
月总收入/元	3384	3346

送餐每单奖励元，送餐员月基本工资为元；

（1）求a、b的值；

（2）若月送餐单数超过300单时，超过部分每单的奖金增加1元．假设月送餐单数为单，月总收入为元，请写出与的函数关系式，若送餐员小李计划月收入不低于5200元，那么他每月至少要送多少单？

【题目】四边形 ABCD 中，E 为边 BC 上一点，F 为边 CD 上一点，且∠AEF=90°．

（1）如图 1，若 ABCD 为正方形，E 为 BC 中点，求证：．

（2）若 ABCD 为平行四边形，∠AFE=∠ADC，

①如图 2，若∠AFE=60°，求的值；

②如图 3，若 AB=BC，EC=2CF．直接写出 cos∠AFE 值为　　　．

【题目】如图，在ABCD中，AB=1，BC=，对角线AC，BD交于O点，将直线AC绕点O顺时针旋转，分别交于BC，AD于点E，F．

（1）证明：当旋转角为　　时，四边形ABEF是平行四边形；

（2）在旋转过程中，四边形BEDF可能是菱形吗？如果不可能，请说明理由；如果可能，说明理由并求出此时AC绕点O顺时针旋转的度数．

【题目】对于平面直角坐标系中的点和半径为1的，定义如下：

①点的“派生点”为；

②若上存在两个点，使得，则称点为的“伴侣点”．

应用：已知点

（1）点的派生点坐标为________；在点中，的“伴侣点”是________；

（2）过点作直线交轴正半轴于点，使，若直线上的点是的“伴侣点”，求的取值范围；

（3）点的派生点在直线，求点与上任意一点距离的最小值．

【题目】如图1，在Rt△ADE中，∠DAE=90°，C是边AE上任意一点（点C与点A、E不重合），以AC为一直角边在Rt△ADE的外部作Rt△ABC，∠BAC=90°，连接BE、CD．

（1）在图1中，若AC=AB，AE=AD，现将图1中的Rt△ADE绕着点A顺时针旋转锐角α，得到图2，那么线段BE．CD之间有怎样的关系，写出结论，并说明理由；

（2）在图1中，若CA=3，AB=5，AE=10，AD=6，将图1中的Rt△ADE绕着点A顺时针旋转锐角α，得到图3，连接BD、CE．

①求证：△ABE∽△ACD；

②计算：BD2+CE2的值．

【题目】在矩形ABCD中作图：①分别以点B，C为圆心，BC长为半径画弧，分别交AD于点H，G；②分别以点B，C为圆心，大于BC的一半长为半径画弧，两弧相交于点E，F；③作直线EF，交AD于点P．下列结论不一定成立的是（）

A.BC＝BHB.CG＝AD

C.PB＝PCD.GH＝2AB

【题目】小张骑自行车匀速从甲地到乙地，在途中因故停留了一段时间后，仍按原速骑行，小李骑摩托车比小张晚出发一段时间，以800米/分的速度匀速从乙地到甲地，两人距离乙地的路程(米)与小张出发后的时间 (分)之间的函数图象如图所示.

(1)求小张骑自行车的速度；

(2)求小张停留后再出发时与之间的函数表达式:.

(3)求小张与小李相遇时的值.

试题分类