题目内容
【题目】已知在平行四边形![]() 中,点
中,点![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 于点
于点![]() ,
,
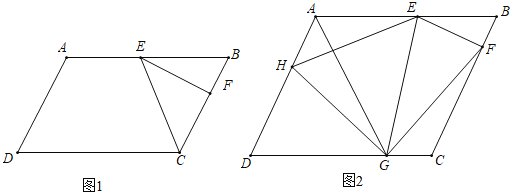
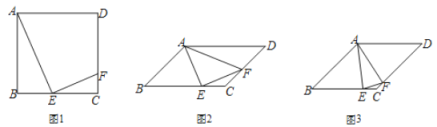
(1)如图1,连接![]() ,若点
,若点![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
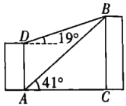
(2)如图2,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 为等边三角形,且
为等边三角形,且![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)11;(2)见解析
【解析】
(1)解直角三角形求出BF,CF,即可解决问题.
(2)作GT∥CB交AB于T,交EF于K.证明△AGT是等边三角形,得出AT=AG,再证明△AGH≌△TGE(SAS),得出AH=TE,即可得出结论.
(1)∵四边形ABCD是平行四边形,
∴AB=CD=10,BC=AD,
∵点![]() 为
为![]() 中点,
中点,
∴AE=EB=5,
∵EF⊥BF,tanB=![]() ,
,
设EF=4x,则BF=3x,
在Rt△BEF中,由勾股定理得:(4x)2+(3x)2=52,
解得:x=1,
∴EF=4,BF=3,
在Rt△ECF中,CF=![]() ,
,
∴BC=BF+CF=11,
∴AD=BC=11;
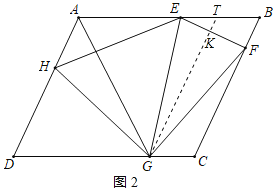
(2)如图2中,作GT∥CB交AB于T,交EF于K.
则∠FGT=∠GFC,
∵∠EGF=2∠GFC,
∴∠TGE=∠GFC=∠FGT,
∵∠AGH=∠GFC,
∴∠TGE=∠AGH,
∴∠AGT=∠AGE+∠EGT=∠AGE+∠AGH=∠EGH
∵△EGH是等边三角形,
∴GE=GH,∠EGH =60°,
∴∠AGT==60°
∵FG⊥GH,
∴∠FGH=90°,
∴∠EGF=30°,
∵∠EGF=2∠GFC,
∴∠GFC=∠EGT =15°,
∵GT∥BC,EF⊥BC,
∴EF⊥GT,
∴∠GKE=∠EKT=90°,
∴∠GEF=90°-∠EGT=75°,
∵EG平分∠AEF
∴∠AEG=∠GEF=75°,
∴∠BEF=30°,
∴∴∠ATG =90°-30°=60°,
∴△AGT是等边三角形,
∴AT=AG=TG,
在△AGH和△TGE中,
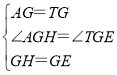 ,
,
∴△AGH≌△TGE(SAS),
∴AH=TE,
∵AE+TE=AT,
∴AE+AH=AG.

【题目】为调动学生学习积极性,某中学初一(1)班对学生的学习表现实行每学月评分制,现对初一上期1—5学月的评分情况进行了统计,其中学生小明5次得分情况如下表所示:
时间 | 第1学月 | 第2学月 | 第3学月 | 第4学月 | 第5学月 |
得分 | 8分 | 9分 | 9分 | 9分 | 10分 |
学生小刚的得分情况制成了如下不完整的折线统计图:
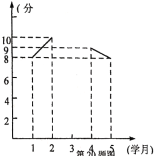
(1)若小刚和小明这5次得分的平均成绩相等,求出小刚第3学月的得分,并补全折线统计图;
(2)据统计,小明和小刚这5学月的总成绩都排在了班级的前4名,现准备从该班的前四名中任选两名同学参加学校的表彰大会,请用列表或画树状图的方法,求选取的两名同学恰好是小明和小刚两人的概率.