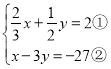题目内容
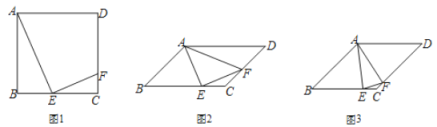
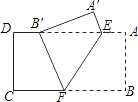
【题目】如图,点![]() 是矩形
是矩形![]() 中
中![]() 边上一点,
边上一点,![]() 沿
沿![]() 折叠为
折叠为![]() ,点
,点![]() 落在
落在![]() 上.
上.
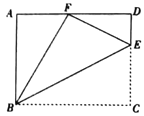
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,是否存在
,是否存在![]() 的值,使
的值,使![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见详解;(2)![]() ;(3)存在,
;(3)存在,![]() 时,
时,![]() 与
与![]() 相似
相似
【解析】
(1)由矩形的性质可知∠A=∠D=90°,由等角的余角相等可得出∠ABF=∠DFE,进而可证出△ABF∽△DFE;
(2)设设![]() ,
,![]() ,
,![]() ,利用折叠的性质可得出
,利用折叠的性质可得出![]() ,
,![]() ,
,![]() ,
,![]() ,利用相似三角形的性质可得出
,利用相似三角形的性质可得出![]() ,再结合正切的定义即可求出
,再结合正切的定义即可求出![]() 的值;
的值;
(3)分当![]() 时和当
时和当![]() 时两种情况讨论即可得出答案.
时两种情况讨论即可得出答案.
(1)证明:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() 沿
沿![]() 折叠为
折叠为![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
∴![]() ;
;
(2)解:在![]() 中,
中,![]() ,
,
∴设![]() ,
,![]() ,
,![]() ,
,
∵![]() 沿
沿![]() 折叠为
折叠为![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ;
;
(3)存在,![]() 时,
时,![]() 与
与![]() 相似
相似
理由:当![]() 时,
时,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
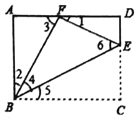
②当![]() 时,
时,![]() ,∵
,∵![]() ,∴
,∴![]() ,这与
,这与![]() 相矛盾,
相矛盾,
∴![]() 不成立.
不成立.
综上所述,![]() 时,
时,![]() 与
与![]() 相似.
相似.

练习册系列答案
相关题目