题目内容
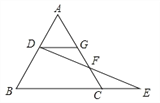
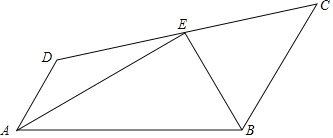
【题目】如图，四边形ABCD中，AD∥BC，点E在CD上，EA，EB分别平分∠DAB和∠CBA，设AD＝x，BC＝y且（x﹣3）2+|y﹣4|＝0．求AB的长．
【答案】7
【解析】
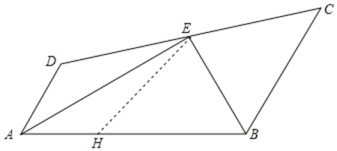
由非负性可求AD＝3，BC＝4，如图，在AB上截取AH＝AD＝3，连接HE，由“SAS”可证△DAE≌△HAE，可得∠DEA＝∠AEH，由“ASA”可证△BEH≌△BEC，可得BH＝BC＝4，即可求解．
∵（x﹣3）2+|y﹣4|＝0，
∴x-3=0，y-4=0，
∴x＝3，y＝4，
∴AD＝3，BC＝4，
如图，在AB上截取AH＝AD＝3，连接HE，
∵AD∥BC，
∴∠DAB+∠ABC＝180°，
∵EA，EB分别平分∠DAB和∠CBA，
∴∠DAE＝∠EAB＝
∠DAB，∠EBC＝∠EBA＝∠ABC，
∴∠EAB+∠EBA＝90°，
∴∠AEB＝90°，
∴∠DEA+∠BEC＝90°，
∵∠DAE＝∠EAH，AD＝AH，AE＝AE，
∴△DAE≌△HAE（SAS）
∴∠DEA＝∠AEH，
∵∠AEH+∠BEH＝90°，∠DEA+∠BEC＝90°，
∴∠HEB＝∠CEB，且BE＝BE，∠CBE＝∠HBE，
∴△BEH≌△BEC（ASA）
∴BH＝BC＝4，
∴AB＝AH+BH＝7．
练习册系列答案
相关题目
