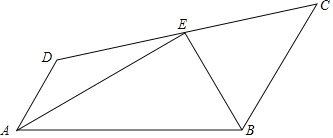
题目内容
【题目】已知:如图,点D在等边△ABC的边AB上,作DG∥BC,交AC于点G,点F在边AC上,连接DF并延长,交BC的延长线于点E,FE=FD.求证:AD=CE.
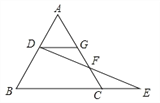
【答案】证明见解析.
【解析】首先通过平行线证明△DFG和△EFC全等,从而得出△ABC为等边三角形,然后根据角度之间的关系得出△ADG也是等边三角形,从而得出答案.
证明:∵DG∥BC,∴∠DGF=∠ECF,在△DFG和△EFC中,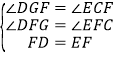 ,
,
∴△DFG≌△EFC(AAS), ∴GD=CE,∵△ABC是等边三角形, ∴∠A=∠B=∠ACB=60,
∵DG∥BC,∴∠ADG=∠B,∠AGD=∠ACB,∴∠A=∠ADG=∠AGD,∴△ADG是等边三角形,
∴AD=GD, ∴AD=CE.

练习册系列答案
相关题目
【题目】小明买了张100元的乘车IC卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y元)如表:
次数x | 1 | 2 | 3 | 4 | … |
余额y | 100-1.2 | 100-2.4 | 100-3.6 | 100-4.8 | … |
(1)写出乘车的次数x表示余额y的关系式.
(2)利用上述关系式计算小明乘了15次车还剩下多少元?
(3)余额还有40元时,小明已使用此卡乘车多少次?
(4)小强最多能乘几次车?