题目内容
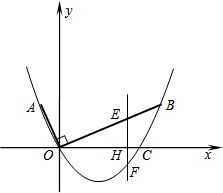 如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)①连结AB,则AB与x轴的位置关系是
(4)点E为线段OB上一动点,过点EF∥y轴,交x轴于点H,交抛物线于点F,EF是否有最大值?如有直接出点E的坐标及最大值;若没有,请说明理由.
考点:二次函数综合题
专题:综合题
分析:(1)过点A作AM⊥x轴于点M,作BN⊥x轴于点N,则∠OAM=∠OBN,证明△OAM∽△BON,可得ON,BN的值,继而得出点B的坐标;
(2)利用待定系数法求解过点A、O、B的抛物线的表达式;
(3)①根据A、B的纵坐标相等,可判断AB与x轴平行;②要使S△ABP=S△ABO,需要满足点P到AB的距离等于点O到AB的距离,得出点P的纵坐标即可求出点P的横坐标;
(4)先求出OB的解析式,设点E的坐标,则可表示出点E、点F的纵坐标,表示出EF的长,利用配方法求最值即可.
(2)利用待定系数法求解过点A、O、B的抛物线的表达式;
(3)①根据A、B的纵坐标相等,可判断AB与x轴平行;②要使S△ABP=S△ABO,需要满足点P到AB的距离等于点O到AB的距离,得出点P的纵坐标即可求出点P的横坐标;
(4)先求出OB的解析式,设点E的坐标,则可表示出点E、点F的纵坐标,表示出EF的长,利用配方法求最值即可.
解答:解:(1)过点A作AM⊥x轴于点M,作BN⊥x轴于点N,
则∠OAM=∠BON(都是∠AOM的余角),
∴△OAM∽△BON,
又∵∠AMO=∠ONB=90°,
∴△OAM∽△BON,
∴
=
=
=
,
∴ON=2AM=4,BN=2OM=2,
∴点B的坐标为(4,2);
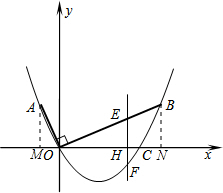
(2)设过点A、O、B三点的抛物线解析式为y=ax2+bx,
将点A、B的坐标代入可得:
,
解得:
,
∴抛物线解析式为y=
x2-
x;
(3)①∵AM=BN,
∴AB与x轴平行;
②∵S△ABP=S△ABO,
∴点P到AB的距离等于点O到AB的距离,
∴点P的纵坐标为0或4,
①当点P的纵坐标为0时,点P与点C重合,
此时点P的坐标为(
,0);
②当点P的纵坐标为4时,
x2-
x=4,
解得:x1=
,x2=
,
∴点P的坐标为(
,4)或(
,4).
综上可得点P的坐标为(
,0),(
,4),(
,4)时,使得S△ABP=S△ABO;
(4)设直线OB的解析式为y=kx,
将点B的坐标代入得:2=4k,
解得:k=
,
∴OB的解析式为y=
x,
设点E的坐标为(x,
x),则点F的坐标为(x,
x2-
x),
则EF=
x-(
x2-
x)=-
x2+
x=-
(x-1)2+
,
∴当x=1时,EF取得最大值,
此时点E的坐标为(1,2).
则∠OAM=∠BON(都是∠AOM的余角),
∴△OAM∽△BON,
又∵∠AMO=∠ONB=90°,
∴△OAM∽△BON,
∴
| AM |
| ON |
| OM |
| BN |
| AO |
| OB |
| 1 |
| 2 |
∴ON=2AM=4,BN=2OM=2,
∴点B的坐标为(4,2);

(2)设过点A、O、B三点的抛物线解析式为y=ax2+bx,
将点A、B的坐标代入可得:
|
解得:
|
∴抛物线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(3)①∵AM=BN,
∴AB与x轴平行;
②∵S△ABP=S△ABO,
∴点P到AB的距离等于点O到AB的距离,
∴点P的纵坐标为0或4,
①当点P的纵坐标为0时,点P与点C重合,
此时点P的坐标为(
| 1 |
| 2 |
②当点P的纵坐标为4时,
| 1 |
| 2 |
| 3 |
| 2 |
解得:x1=
3+
| ||
| 2 |
3-
| ||
| 2 |
∴点P的坐标为(
3+
| ||
| 2 |
3-
| ||
| 2 |
综上可得点P的坐标为(
| 1 |
| 2 |
3+
| ||
| 2 |
3-
| ||
| 2 |
(4)设直线OB的解析式为y=kx,
将点B的坐标代入得:2=4k,
解得:k=
| 1 |
| 2 |
∴OB的解析式为y=
| 1 |
| 2 |
设点E的坐标为(x,
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
则EF=
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
∴当x=1时,EF取得最大值,
此时点E的坐标为(1,2).
点评:本题考查了二次函数的综合,涉及了待定系数法求抛物线解析式、相似三角形的判定与性质及配方法求二次函数的最值,综合考察的知识点较多,解答此类题目的关键是数形结合思想及分类讨论思想的综合运用,将所学知识融会贯通.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
方程x(x-2)+x-2=0的解为( )
| A、x=2 |
| B、x1=2,x2=1 |
| C、x=-1 |
| D、x1=2,x2=-1 |
在半径为5cm的⊙O中,有长为5cm的弦AB,则O到AB的距离等于( )
A、5
| ||||
B、5
| ||||
C、
| ||||
D、
|
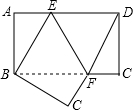 如图,长方形纸片ABCD中,AD=9,AB=3,将其折叠,使其点D与B重合,折痕为EF,则DE和EF长分别为( )
如图,长方形纸片ABCD中,AD=9,AB=3,将其折叠,使其点D与B重合,折痕为EF,则DE和EF长分别为( )A、4,
| ||
B、4,2
| ||
C、5,
| ||
D、5,2
|