题目内容
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交 ![]() 于点E,以点C为圆心,OA的长为直径作半圆交CE于点D.若OA=4,则图中阴影部分的面积为( )
于点E,以点C为圆心,OA的长为直径作半圆交CE于点D.若OA=4,则图中阴影部分的面积为( )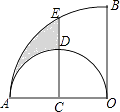
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】连接OE,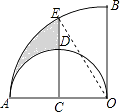
∵C为OA的中点,OC⊥OA且OA=4,
∴OC=2,
∴ ![]() ,
, ![]() .,
.,
∴cos∠COE=60°.
∵∠AOB=90°,
∴∠BOE=30°,
∴ ![]()
![]()
![]()
![]()
故答案为:D.
连接OE,得出S阴影=S扇形AOBS扇形ACDS扇形BOES△COE , 先根据已知求出OC的长,再在Rt△OCD中,利用三角函数的定义及特殊角的三角函数值求出∠COE的度数,从而求出∠BOE的度数,然后利用扇形的面积公式及三角形的面积公式分别求出扇形AOB、扇形ACD、扇形BOE、△COE的面积,即可求出答案。

练习册系列答案
相关题目