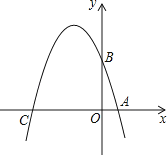题目内容
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)b= , c= , 点B的坐标为;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
【答案】
(1)-2;-3;(﹣1,0)
(2)
解:存在.
理由:如图所示:

①当∠ACP1=90°.
由(1)可知点A的坐标为(3,0).
设AC的解析式为y=kx﹣3.
∵将点A的坐标代入得3k﹣3=0,解得k=1,
∴直线AC的解析式为y=x﹣3.
∴直线CP1的解析式为y=﹣x﹣3.
∵将y=﹣x﹣3与y=x2﹣2x﹣3联立解得x1=1,x2=0(舍去),
∴点P1的坐标为(1,﹣4).
②当∠P2AC=90°时.
设AP2的解析式为y=﹣x+b.
∵将x=3,y=0代入得:﹣3+b=0,解得b=3.
∴直线AP2的解析式为y=﹣x+3.
∵将y=﹣x+3与y=x2﹣2x﹣3联立解得x1=﹣2,x2=3(舍去),
∴点P2的坐标为(﹣2,5).
综上所述,P的坐标是(1,﹣4)或(﹣2,5).
(3)
解:如图2所示:连接OD.

由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短.
由(1)可知,在Rt△AOC中,
∵OC=OA=3,OD⊥AC,
∴D是AC的中点.
又∵DF∥OC,
∴DF= ![]() OC=
OC= ![]() .DF=
.DF= ![]() OC=
OC= ![]()
∴点P的纵坐标是- ![]() .
.
∴ ![]() ,解得:
,解得: ![]() .
.
∴当EF最短时,点P的坐标是:( ![]() ,-
,- ![]() )或(
)或( ![]() ,-
,- ![]() ).
).
【解析】解:(1)∵将点A和点C的坐标代入抛物线的解析式得: ![]() ,解得:b=﹣2,c=﹣3.
,解得:b=﹣2,c=﹣3.
∴抛物线的解析式为y=x2﹣2x﹣3.
∵令x2﹣2x﹣3=0,解得:x1=﹣1,x2=3.
∴点B的坐标为(﹣1,0).
所以答案是:﹣2;﹣3;(﹣1,0).
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点和垂线段最短的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用.

【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |

(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.