题目内容
【题目】如图，在矩形ABCD中，AB=5，BC=10 
，一圆弧过点B和点C，且与AD相切，则图中阴影部分面积为 ． 
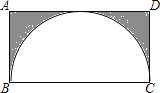
【答案】75 
﹣ 
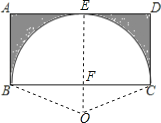
【解析】解：设圆弧的圆心为O，与AD切于E，
连接OE交BC于F，连接OB、OC，
设圆的半径为x，则OF=x﹣5，
由勾股定理得，OB2=OF2+BF2 ，
即x2=（x﹣5）2+（5 ）2 ，
解得，x=5，
则∠BOF=60°，∠BOC=120°，
则阴影部分面积为：矩形ABCD的面积﹣（扇形BOCE的面积﹣△BOC的面积）
=10 ×5﹣ 
+ 
×10 ×5=75 ﹣ ，
所以答案是：75 ﹣ ．
【考点精析】本题主要考查了矩形的性质和切线的性质定理的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．
练习册系列答案
相关题目
