��Ŀ����
����Ŀ����ͼ��������y=ax2+bx��3a��a��0����x�ύ�ڵ�A����1��0���͵�B����y�ύ�ڵ�C��0��2��������BC��
��1����������ߵĽ���ʽ�ͶԳ��ᣬ��д���߶�BC���е����ꣻ
��2�����߶�BC������ƽ��2����λ���ȣ�������ƽ��m����λ���ȣ�ʹ��C�Ķ�Ӧ��C1ǡ�����ڸ��������ϣ����ʱ��C1�������m��ֵ��
��3������P�Ǹ��������ϵĶ��㣬��Q�Ǹ������߶Գ����ϵĶ��㣬����P��Q��B��C�ĵ�Ϊ������ı�����ƽ���ı���ʱ�����ʱ��P�����꣮
���𰸡�
��1��
�⣺��������y=ax2+bx��3a��a��0����x�ύ�ڵ�A����1��0���͵�B����y�ύ�ڵ�C��0��2����
�� ![]() ��
��
��� 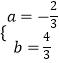 ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x+2=��
x+2=�� ![]() ��x��1��2+2
��x��1��2+2 ![]() ��
��
��Գ�����x=1��
��1+��1+1��=3��
��B��������3��0����
��BC���е�����Ϊ��1.5��1��
��2��
�⣺���߶�BC������ƽ��2����λ���ȣ�������ƽ��m����λ���ȣ�ʹ��C�Ķ�Ӧ��C1ǡ�����ڸ��������ϣ�
���C1�ĺ�����Ϊ��2��
��x=��2ʱ��y=�� ![]() ������2��2+
������2��2+ ![]() ������2��+2=��
������2��+2=�� ![]() ��
��
���C1����������2���� ![]() ����
����
m=2������ ![]() ��=5
��=5 ![]()
��3��
�⣺����BCΪƽ���ı��ε�һ�ߣ�
��BC�ĺ�����IJ�Ϊ3��
�ߵ�Q�ĺ�����Ϊ1��
��P�ĺ�����Ϊ4��2��
��P���������ϣ�
��P����������3 ![]() ��
��
��P1��4����3 ![]() ����P2����2����3
����P2����2����3 ![]() ����
����
����BCΪƽ���ı��εĶԽ��ߣ�
��BC��PQ����ƽ�֣�
�ߵ�Q�ĺ�����Ϊ1��BC���е�����Ϊ��1.5��1����
��P��ĺ�����Ϊ1.5+��1.5��1��=2��
��P���������� ![]() ��22+
��22+ ![]() ��2+2=2��
��2+2=2��
��P3��2��2����
������������P��������P1��4����3 ![]() ����P2����2����3
����P2����2����3 ![]() ����P3��2��2��
����P3��2��2��
����������1���ѵ�A����1��0���͵�C��0��2��������������������߿ɵ�a��b��ֵ�������õ��������ߵĽ���ʽ�ͶԳ��ᣬ�������B�����꣬�����е����깫ʽ����߶�BC���е����꼴�ɣ���2������ƽ�Ƶ����ʿ�֪����C�Ķ�Ӧ��C1�ĺ�����Ϊ��2���ٴ��������߿����C1�����꣬��һ���õ�m��ֵ����3��B��CΪ���㣬�ɷ�BCΪƽ���ı��ε�һ���Խ����������̽�ֵõ���P�����꣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

����Ŀ������ij��ҵ������һ��������Ŀ��Ϊ�˽�Լ��Դ����������������ҵ��������A��B�����ͺŵ���ˮ�����豸��10̨������������±���
A�� | B�� | |
�۸���Ԫ/̨�� | 15 | 12 |
����ˮ������������/�£� | 250 | 200 |
��Ԥ�㣬��ҵ���֧��136��Ԫ�����豸����Ҫ���´�����ˮ����������2150�֣�
��1������ҵ���ļ��ֹ�����
��2�����ַ�����ʡǮ����˵�����ɣ�