Question

【题目】如图，已知点A1的坐标为（0，1），直线1为y=x．过点A1作A1B1⊥y轴交直线1于点B1，过点B1作A2B1⊥1交y轴于点A2；过点A2作A2B2⊥y轴交直线1于点B2，过点B2作A3B2⊥1交y轴于点A3，……，则AnBn的长是______．

Answer 1

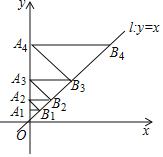
【答案】2n-1

【解析】

由点A1的坐标可得出点B1的坐标，进而可得出A1B1的长，由A2B1⊥1交y轴于点A2结合直线1为y=x可得出△A1A2B1为等腰直角三角形，根据等腰直角三角形的性质可得出点A2的坐标，利用一次函数图象上点的坐标可得出点B2的坐标，进而可得出A2B2的长，同理，可得出A3B3，A4B4，…的长，再根据各线段长度的变化可找出变化规律“AnBn=2n-1”，此题得解．

解：∵点A1的坐标为（0，1），

∴点B1的坐标为（1，1），A1B1=1．

∵A2B1⊥1交y轴于点A2，直线1为y=x，

∴△A1A2B1为等腰直角三角形，

∴点A2的坐标为（0，2），点B2的坐标为（2，2），

∴A2B2=2．

同理，可得：A3B3=4，A4B4=8，…，

∴AnBn=2n-1．

故答案为：2n-1．