题目内容
、如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.
小题1:点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.
小题2:点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形?
小题3:若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,并证明你的猜想.
小题1:点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.
小题2:点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形?
小题3:若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,并证明你的猜想.

小题1:AE=AD
小题2:菱形
小题3:OC = AC+AD
(1) AE=AD
理由:AC⊥OM
在Rt△AOE中,∠AEO+∠AOE=900
同理:∠ODB+∠DOB=900
又∵∠MON的角平分线OP分别交AB于D点.
∴∠AEO=∠DOB
又∵∠DOB=∠ADE
∴∠AED=∠ADE
∴AE=AD
(2)菱形
证明: 连接AF交DE于点G,连接DF,EF.
点F与点A关于直线OP对称可知:AF⊥DE, AE=FE,
∴AG=FG,
又∵AE=AD
∴DG=EG
∴四边形ADFE是平行四边形
∵AF⊥DE
∴平行四边形ADFE是菱形
(3)OC= AC+AD
证明:连接EF.
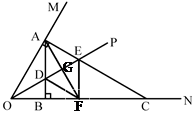
∵点F与点A关于直线OP对称,
∴AO=OF
∵AC⊥OM, ∠MON=45°
∴∠OAC=90°
∴∠ACO=∠MON=45°
∴OF =" AO" = AC
由(2)知四边形ADFE是菱形
∴EF∥AB AD=EF
∵AB⊥ON
∴∠ABC=90°
∴∠EFC=∠ABC =90°
∵∠ACO=45°
∴∠ACO=∠CEF
∴FC =" EF" =AD
又∵OC=OF+FC
∴OC = AC+AD
理由:AC⊥OM
在Rt△AOE中,∠AEO+∠AOE=900
同理:∠ODB+∠DOB=900
又∵∠MON的角平分线OP分别交AB于D点.
∴∠AEO=∠DOB
又∵∠DOB=∠ADE
∴∠AED=∠ADE
∴AE=AD
(2)菱形
证明: 连接AF交DE于点G,连接DF,EF.
点F与点A关于直线OP对称可知:AF⊥DE, AE=FE,
∴AG=FG,
又∵AE=AD
∴DG=EG
∴四边形ADFE是平行四边形
∵AF⊥DE
∴平行四边形ADFE是菱形
(3)OC= AC+AD
证明:连接EF.

∵点F与点A关于直线OP对称,
∴AO=OF
∵AC⊥OM, ∠MON=45°
∴∠OAC=90°
∴∠ACO=∠MON=45°
∴OF =" AO" = AC
由(2)知四边形ADFE是菱形
∴EF∥AB AD=EF
∵AB⊥ON
∴∠ABC=90°
∴∠EFC=∠ABC =90°
∵∠ACO=45°
∴∠ACO=∠CEF
∴FC =" EF" =AD
又∵OC=OF+FC
∴OC = AC+AD

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
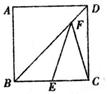


 ,求菱形ADCE的周长.(5分)
,求菱形ADCE的周长.(5分)
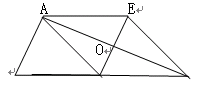
 、
、 是两条对角线,现从以下四个关系式 ①
是两条对角线,现从以下四个关系式 ① ,②
,② ,③
,③ ,④
,④ 中、任取一个作为条件,即可推出平行四边形
中、任取一个作为条件,即可推出平行四边形 是矩形的概率为 。
是矩形的概率为 。