МвДҝДЪИЭ
ЎҫМвДҝЎҝИзНјЈ¬![]() ЦР,ЎПC=90Ўг,
ЦР,ЎПC=90Ўг,![]() ,
,![]() ,Иф¶ҜөгPҙУөгCҝӘКј,°ҙ
,Иф¶ҜөгPҙУөгCҝӘКј,°ҙ![]() өДВ·ҫ¶ФЛ¶Ҝ,ЗТЛЩ¶ИОӘГҝГл1cm,Йиіц·ўөДКұјдОӘtГлЈ®
өДВ·ҫ¶ФЛ¶Ҝ,ЗТЛЩ¶ИОӘГҝГл1cm,Йиіц·ўөДКұјдОӘtГлЈ®
![]() өгPіц·ў2Гләу,ЗуCPәНBPөДіӨЈ®
өгPіц·ў2Гләу,ЗуCPәНBPөДіӨЈ®
![]() ОКtВъЧгКІГҙМхјюКұ
ОКtВъЧгКІГҙМхјюКұ![]() өДЦө»тИЎЦө·¶О§
өДЦө»тИЎЦө·¶О§![]() ,
,![]() ОӘЦұҪЗИэҪЗРОЈҝ
ОӘЦұҪЗИэҪЗРОЈҝ
![]() БнУРТ»өгQ,ҙУөгCҝӘКј,°ҙ
БнУРТ»өгQ,ҙУөгCҝӘКј,°ҙ![]() өДВ·ҫ¶ФЛ¶Ҝ,ЗТЛЩ¶ИОӘГҝГл2cm,ИфPЎўQБҪөгН¬Кұіц·ў,өұPЎўQЦРУРТ»өгөҪҙпЦХөгКұ,БнТ»өгТІНЈЦ№ФЛ¶Ҝ
өДВ·ҫ¶ФЛ¶Ҝ,ЗТЛЩ¶ИОӘГҝГл2cm,ИфPЎўQБҪөгН¬Кұіц·ў,өұPЎўQЦРУРТ»өгөҪҙпЦХөгКұ,БнТ»өгТІНЈЦ№ФЛ¶Ҝ![]() өұtОӘәОЦөКұ,ЦұПЯPQ°С
өұtОӘәОЦөКұ,ЦұПЯPQ°С![]() өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·ЦЈҝ
өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·ЦЈҝ
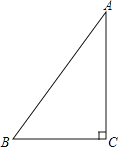
Ўҫҙр°ёЎҝ(1)PB=![]() cmЈ»CP=2cmЈ»(2)
cmЈ»CP=2cmЈ»(2)![]() »т
»т![]() Ј»(3)
Ј»(3)![]() »т6Гл.
»т6Гл.
ЎҫҪвОцЎҝ
![]() КЧПИАыУГ№ҙ№Й¶ЁАнјЖЛгіцACіӨ,ёщҫЭМвТвҝЙөГ
КЧПИАыУГ№ҙ№Й¶ЁАнјЖЛгіцACіӨ,ёщҫЭМвТвҝЙөГ![]() ,ФЩАыУГ№ҙ№Й¶ЁАнјЖЛгіцPBөДіӨ,Ҫш¶шҝЙөГ
,ФЩАыУГ№ҙ№Й¶ЁАнјЖЛгіцPBөДіӨ,Ҫш¶шҝЙөГ![]() өДЦЬіӨЈ»
өДЦЬіӨЈ»
![]() өұPФЪACЙПФЛ¶ҜКұ
өұPФЪACЙПФЛ¶ҜКұ![]() ОӘЦұҪЗИэҪЗРО,УЙҙЛҝЙөГ
ОӘЦұҪЗИэҪЗРО,УЙҙЛҝЙөГ![]() Ј»өұPФЪABЙПКұ,
Ј»өұPФЪABЙПКұ,![]() Кұ,
Кұ,![]() ОӘЦұҪЗИэҪЗРО,КЧПИјЖЛгіцCPөДіӨ,И»әуФЩАыУГ№ҙ№Й¶ЁАнјЖЛгіцAPіӨ,Ҫш¶шҝЙөГҙр°ёЈ®
ОӘЦұҪЗИэҪЗРО,КЧПИјЖЛгіцCPөДіӨ,И»әуФЩАыУГ№ҙ№Й¶ЁАнјЖЛгіцAPіӨ,Ҫш¶шҝЙөГҙр°ёЈ®
![]() ·ЦАаМЦВЫЈәөұPөгФЪACЙП,QФЪABЙП,Фт
·ЦАаМЦВЫЈәөұPөгФЪACЙП,QФЪABЙП,Фт![]() ,
,![]() ,
,![]() Ј»өұPөгФЪABЙП,QФЪACЙП,Фт
Ј»өұPөгФЪABЙП,QФЪACЙП,Фт![]() ,
,![]() ,
,![]() Ј®
Ј®
(1)ЎЯЎПC=90Ўг,![]() ,
,![]() ,
,
![]() ,¶ҜөгPҙУөгCҝӘКј,°ҙ
,¶ҜөгPҙУөгCҝӘКј,°ҙ![]() өДВ·ҫ¶ФЛ¶Ҝ,ЛЩ¶ИОӘГҝГл1cm,
өДВ·ҫ¶ФЛ¶Ҝ,ЛЩ¶ИОӘГҝГл1cm,
![]() іц·ў2Гләу,Фт
іц·ў2Гләу,Фт![]() ,
,
ЎЯЎПC=90Ўг,
![]() ,
,
![]() ,¶ҜөгPҙУөгCҝӘКј,°ҙ
,¶ҜөгPҙУөгCҝӘКј,°ҙ![]() өДВ·ҫ¶ФЛ¶Ҝ,ЗТЛЩ¶ИОӘГҝГл1cm,
өДВ·ҫ¶ФЛ¶Ҝ,ЗТЛЩ¶ИОӘГҝГл1cm,
![]() ФЪACЙПФЛ¶ҜКұ
ФЪACЙПФЛ¶ҜКұ![]() ОӘЦұҪЗИэҪЗРО,
ОӘЦұҪЗИэҪЗРО,
![]() ,
,
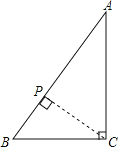
ИзНјЈ¬өұPФЪABЙПКұ,![]() Кұ,
Кұ,![]() ОӘЦұҪЗИэҪЗРО,
ОӘЦұҪЗИэҪЗРО,
![]() ,
,
![]() ,
,
ҪвөГЈә![]() ,
,
![]() ,
,
![]() ,
,
![]() ЛЩ¶ИОӘГҝГл1cm,
ЛЩ¶ИОӘГҝГл1cm,
![]() ,
,
ЧЫЙПЛщКцЈәөұ![]() »т
»т![]() ,
,![]() ОӘЦұҪЗИэҪЗРОЈ»
ОӘЦұҪЗИэҪЗРОЈ»
![]() өұPөгФЪACЙП,QФЪABЙП,Фт
өұPөгФЪACЙП,QФЪABЙП,Фт![]() ,
,![]() ,
,
![]() ЦұПЯPQ°С
ЦұПЯPQ°С![]() өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц,
өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц,
![]() ,
,![]() Ј»
Ј»
өұPөгФЪABЙП,QФЪACЙП,Фт![]() ,
,![]() ,
,
![]() ЦұПЯPQ°С
ЦұПЯPQ°С![]() өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц,
өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц,
![]() ,
,
![]() ,
,
![]() өұ
өұ![]() »т6ГлКұ,ЦұПЯPQ°С
»т6ГлКұ,ЦұПЯPQ°С![]() өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·ЦЈ®
өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·ЦЈ®

 РВұаРЎС§өҘФӘЧФІвМвПөБРҙр°ё
РВұаРЎС§өҘФӘЧФІвМвПөБРҙр°ёЎҫМвДҝЎҝПВұнКЗДіРЈЎ°әУДПКЎәәЧУМэРҙҙуИьіхИьЎұ№ЪҫьЧйіЙФұөДДкБд·ЦІј
ДкБд/Лк | 12 | 13 | 14 | 15 |
ИЛКэ | 5 | 15 | x | 12©Ғx |
¶ФУЪІ»Н¬өДxЈ¬ПВБР№ШУЪДкБдөДНіјЖБҝІ»»б·ўЙъёДұдөДКЗЈЁЎЎЎЎЈ©
A. ЖҪҫщКэЎўЦРО»Кэ B. ЖҪҫщКэЎў·ҪІо C. ЦЪКэЎўЦРО»Кэ D. ЦРО»КэЎў·ҪІо