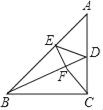
题目内容
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
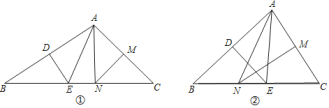
(1)请判断△ANE的周长与AB+AC的和的大小,并说明理由.
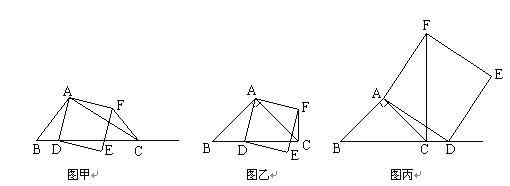
(2)①如图①,若∠B=34°,∠C=28°,求![]() 的度数为______;
的度数为______;
②如图②,若![]() ,则
,则![]() 的度数为________;
的度数为________;
③若![]()
![]() ,则
,则![]() 的度数为________.
的度数为________.
【答案】(1)△ANE的周长<AB+BC;(2)①56°;②16°;③当0°<α<90°时,∠EAN=180°-2α;当180°>α>90°时,∠EAN=2α-180°
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,AN=CN,则△ANE的周长等于BE+EN+AN;
(2)①根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,再根据等边对等角可得∠BAE=∠B,同理可得,∠CAN=∠C,然后利用外角和公式求出∠EAN=180°-2∠B-2∠C,即可求解;
②根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,再根据等边对等角可得∠BAE=∠B,同理可得,∠CAN=∠C,然后利用三角形的内角和定理求出∠B+∠C,再根据∠EAN=∠BAC-(∠BAE+∠CAN)代入数据进行计算即可得解;
③根据前两问的求解方法,分0°<α<90°与180°>α>90°两种情况解答.
解:(1)△ANE的周长<AB+BC,理由如下
∵DE垂直平分AB,![]() 垂直平分
垂直平分![]()
∴AE=BE,AN=CN
又∵△ANE的周长=AE+EN+AN
∴△ANE的周长=AE+EN+AN=BE+EN+CN=BC
∴△ANE的周长<AB+BC
(2)①∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
在三角形AEN中,
∴∠EAN=180°-∠AEN-∠ANE,
又∵∠AEN=∠B+∠BAE, ∠ANE=∠C+∠CAN
∴∠EAN=180°-2∠B-2∠C=56°;
②∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC,
=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=180°-∠BAC=98°,
∴∠EAN=∠BAE+∠CAN-∠BAC=98°-82°=16°;
③∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC,
=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=180°-∠BAC=180°-α,
∴∠EAN=∠BAE+∠CAN-∠BAC=![]() -α=180°-2α
-α=180°-2α
∴当0°<α<90°时,∠EAN=180°-2α;
当180°>α>90°时,∠EAN=2α-180°.

 名校课堂系列答案
名校课堂系列答案