题目内容
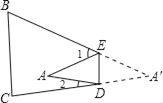
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)设∠AED的度数为x,∠ADE的度数为y,那么∠1、∠2的度数分别是多少?(用含有x或y的代数式表示)
(2)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.
【答案】(1)∠1=(180﹣2x)度,∠2=(180﹣2y)度;(2)∠A=![]() (∠1+∠2).
(∠1+∠2).
【解析】
(1)根据翻折不变性,得到∠AED=∠A′ED,∠ADE=∠A′DE,根据邻补角定义,可得到∠1、∠2的度数(用含有x或y的代数式表示);
(2)根据(1)中结论和三角形的内角和定理即可求出∠A与∠1+∠2之间的数量关系.
(1)∵∠AED=x度,∠ADE=y度,
∴∠AEA′=2x度,∠ADA′=2y度,
∴∠1=(180﹣2x)度,
∠2=(180﹣2y)度;
(2)∵∠1=(180﹣2x)度①,
∠2=(180﹣2y)度②,
由①得,x=(90﹣![]() ∠1),
∠1),
由②得,y=(90﹣![]() ∠2).
∠2).
∠A=180﹣x﹣y=180﹣(90﹣![]() ∠1)﹣(90﹣
∠1)﹣(90﹣![]() ∠2)=
∠2)=![]() (∠1+∠2)度.
(∠1+∠2)度.
∴结论为:∠A=![]() (∠1+∠2).
(∠1+∠2).

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目