题目内容
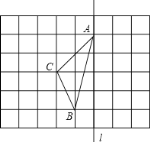
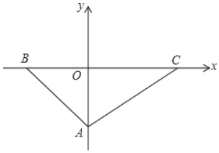
【题目】如图,已知在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
(1)求![]() 三个顶点
三个顶点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,并用含字母
,并用含字母![]() 的式子表示
的式子表示![]() 的面积(
的面积(![]() );
);
(3)在(2)问的条件下,是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积?如果存在,请求出点
的面积?如果存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)A(0,-4),B(-4,0),C(6,0);(2)2a-4或4-2a,详见解析;(3)存在,点P的坐标为(-6,12)或(-6,-8)
【解析】
(1)根据三角形面积公式得到![]() OA2=8,解得OA=4,则OB=OA=4,OC=BC-OB=6,然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标;
OA2=8,解得OA=4,则OB=OA=4,OC=BC-OB=6,然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标;
(2)分类讨论:当点P在在直线AB上方即a>2;当点P在直线AB下方,即a<2;利用面积的和与差求解;
(3)先计算出S△ABC=20,利用(2)中的结果得到方程,然后分别求出a的值,从而确定P点坐标.
解:(1)∵S△ABO=![]() OA×OB,
OA×OB,
∵OA=OB,
∴![]() OA2=8,解得OA=4,
OA2=8,解得OA=4,
∴OB=OA=4,
∴OC=BC-OB=10-4=6,
∴A(0,-4),B(-4,0),C(6,0);
(2)当点P在第二象限,直线AB的上方,即a>2,作PH⊥y轴于H,如图,
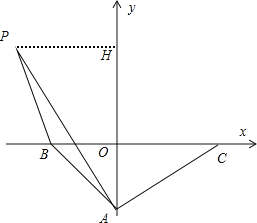
S△PAB=S△AOB+S梯形BOHP-S△PAH=8+![]() (4+6)×a-
(4+6)×a-![]() ×6×(a+4)=2a-4;
×6×(a+4)=2a-4;
当点P在直线AB下方,即a<2,作PH⊥x轴于H,如图,
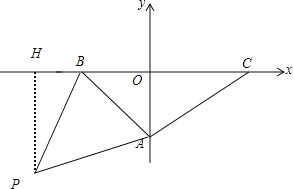
S△PAB=S梯形OHPA-S△PBH-S△OAB=![]() (-a+4)×6-
(-a+4)×6-![]() ×(6-4)×(-a)-8=4-2a;
×(6-4)×(-a)-8=4-2a;
(3)S△ABC=![]() ×10×4=20,
×10×4=20,
当2a-4=20,
解得a=12.
此时P点坐标为(-6,12);
当4-2a=20,
解得a=-8.
此时P点坐标为(-6,-8).
综上所述,点P的坐标为(-6,12)或(-6,-8).

 习题精选系列答案
习题精选系列答案