题目内容
【题目】如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:
①b2>4ac;②ac>0; ③当x>1时,y随x的增大而减小; ④3a+c>0;⑤任意实数m,a+b≥am2+bm.
其中结论正确的序号是( )
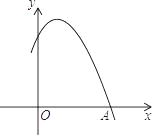
A. ①②③ B. ①④⑤ C. ③④⑤ D. ①③⑤
【答案】D
【解析】
①∵抛物线与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2﹣4ac>0,即b2>4ac,故①正确;
②∵开口向下,与y轴的交点在x轴的上方,
∴a<0,c>0,
∴ac<0,故②错误;
③由图象和二次函数图象的对称轴是x=1,可得当x>1时,y随x的增大而减小,
故③正确;
④∵二次函数y=ax2+bx+c过点A (3,0),对称轴是x=1,
∴抛物线与x轴的另一交点坐标为(﹣1,0),﹣![]() =1,即b=﹣2a,
=1,即b=﹣2a,
∴当x=﹣1时,y=0,即a﹣b+c=0,
∴a+2a+c=0,
∴3a+c=0,
故④错误;
⑤∵二次函数图象的对称轴是x=1,且开口向下,
∴当x=1时,y最大,
∴任意实数m,a+b+c≥am2+bm+c.
即任意实数m,a+b≥am2+bm.
故⑤正确;
故选D.

练习册系列答案
相关题目
【题目】某中学开展“唱红歌”比赛活动,八年级1、2班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据统计图所给的信息填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | 85 | _____ | 85 |
八(2) | _____ | 80 | _____ |
(2)若八(1)班复赛成绩的方差s12=70,请计算八(2)班复赛成绩的方差s22,并说明哪个班级5名选手的复赛成绩更平稳一些.