题目内容
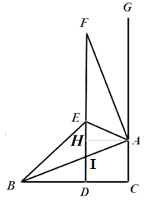
【题目】如图,线段BC=8,射线CG⊥BC,A为射线CG上一点,已知FA⊥AB且FA=AB,AE平分∠FAB,且E点满足∠EBA=∠ABC.

(1)求证:△ABE≌△AFE.
(2)证明:FD⊥BC.
(3)求△BED的周长.
【答案】(1)见解析;(2)见解析;(3)16
【解析】
(1)根据SAS即可证明;
(2)由(1)可得∠F=∠ABE,由已知∠ABE=∠ABC等量代换可得∠F=∠ABC,由对顶角三角形可得∠FDB=∠FAB=90°,即可得出结论;
(3)由(1)可得BE=EF,过A作AH垂直FD,可证△ABC≌△AFH,可得FH=BC=8,再由AH=AC=CD=DH可以推出BD+DF=2BC,即可得出答案.
解:(1)证明:∵AE平分∠FAB,∴∠FAE=∠BAE,
在△BAE和△FAE中
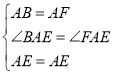 ,
,
∴△BAE≌△FAE(SAS);
(2)证明:∵△BAE≌△FAE,
∴∠F=∠ABE,
∵∠ABE=∠ABC,
∴∠F=∠ABC,
∵∠BID=∠FIA,
∴∠FDB=∠FAB=90°,
即FD⊥BC;
(3)解:∵△BAE≌△FAE,
∴BE=EF,
∴BD+DE+BE=BD+DF,
过A作AH⊥FD于H,
在△ABC与△AFH中,

∴△ABC≌△AFH(AAS),
∴FH=BC=8,
又∵AH=AC=CD=DH,
∴BD+DF=BD+CD+FH=2BC=16,
即△BED的周长为16.

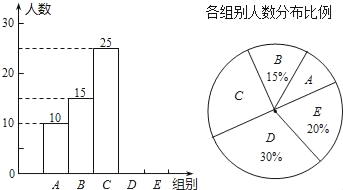
【题目】重庆八中宏帆中学某年级为了选拔参加“全国汉字听写大赛”重庆赛区比赛的队员,特在年级举行全体学生的“汉字听写”比赛,首轮每位学生听写汉字39个.现随机抽取了部分学生的听写结果,绘制成如图的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)已知该年级共有1500名学生,如果听写正确的字的个数不少于24个则进入第二轮的比赛,请你估计本次听写比赛顺利进入第二轮的学生人数;
(3)第二轮比赛过后,为了更有针对性地应对本次大赛,该年级决定从没有担任班主任的5个语文老师(其中3个男老师2个女老师)中随机抽取两个老师对胜出的学生进行培训、辅导.请用树状图或列表法求出抽取的两个老师恰好都是男老师的概率.