题目内容
 (2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
(2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.(1)若折叠后长方体底面正方形的面积为1250cm2,求长方体包装盒的高;
(2)设剪掉的等腰直角三角形的直角边长为x(cm),长方体的侧面积为S(cm2),求S与x的函数关系式,并求x为何值时,S的值最大.
分析:(1)根据等腰直角三角形的性质得出NP的长度,再利用正方形性质表示出底面正方形面积进而得出答案即可;
(2)表示出长方体的侧面积进而利用二次函数的最值求法得出答案.
(2)表示出长方体的侧面积进而利用二次函数的最值求法得出答案.
解答: 解:(1)设剪掉阴影部分的每个等腰直角三角形的腰长为xcm,则NP=
解:(1)设剪掉阴影部分的每个等腰直角三角形的腰长为xcm,则NP=
xcm,
DP=
,QM=PW=
×
,
由题意得:(
×
)2=1250.
解得,x1=5
,x2=55
(超过60,故不符合题意舍去),
答:长方体包装盒的高为5
cm.
另法:∵由已知得底面正方形的边长为
=25
,
∴AN=25
×
=25.
∴PN=60-25×2=10.
∴PQ=10×
=5
(cm).
答:长方体包装盒的高为5
cm.
(2)由题意得,S=4×S四边形QPWM=4×PW•QP,
∵PW=
×
,QP=x,
∴S=4×
×
×x=-4x2+120
x.
∵a=-4<0,
∴当x=15
时,S有最大值.
 解:(1)设剪掉阴影部分的每个等腰直角三角形的腰长为xcm,则NP=
解:(1)设剪掉阴影部分的每个等腰直角三角形的腰长为xcm,则NP=| 2 |
DP=
60-
| ||
| 2 |
| 2 |
60-
| ||
| 2 |
由题意得:(
60-
| ||
| 2 |
| 2 |
解得,x1=5
| 2 |
| 2 |
答:长方体包装盒的高为5
| 2 |
另法:∵由已知得底面正方形的边长为
| 1250 |
| 2 |
∴AN=25
| 2 |
| ||
| 2 |
∴PN=60-25×2=10.
∴PQ=10×
| ||
| 2 |
| 2 |
答:长方体包装盒的高为5
| 2 |
(2)由题意得,S=4×S四边形QPWM=4×PW•QP,
∵PW=
| 2 |
60-
| ||
| 2 |
∴S=4×
| 2 |
60-
| ||
| 2 |
| 2 |
∵a=-4<0,
∴当x=15
| 2 |
点评:本题考查了二次函数的实际应用以及二次函数最值求法,发现底边长与正方形ABCD边长的关系是解题关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
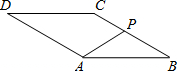 (2012•营口)如图,菱形ABCD的边长为2,∠B=30°.动点P从点B出发,沿B-C-D的路线向点D运动.设△ABP的面积为y(B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )
(2012•营口)如图,菱形ABCD的边长为2,∠B=30°.动点P从点B出发,沿B-C-D的路线向点D运动.设△ABP的面积为y(B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )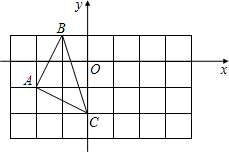 (2012•营口)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).
(2012•营口)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).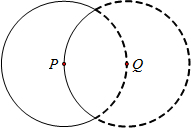 (2012•营口)如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.
(2012•营口)如图,实线部分为某月牙形公园的轮廓示意图,它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成,⊙P与⊙Q的半径都是2km,点P在⊙Q上.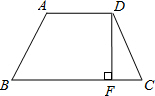 (2012•营口)如图,在等腰梯形ABCD中,AD∥BC,过点D作DF⊥BC于F.若AD=2,BC=4,DF=2,则DC的长为
(2012•营口)如图,在等腰梯形ABCD中,AD∥BC,过点D作DF⊥BC于F.若AD=2,BC=4,DF=2,则DC的长为 (2012•营口)如图,直线
(2012•营口)如图,直线