题目内容
（2012•营口）如图，在等腰梯形ABCD中，AD∥BC，过点D作DF⊥BC于F．若AD=2，BC=4，DF=2，则DC的长为| 5 |
| 5 |
分析：过A作AE⊥BC于E，得出四边形AEFD是平行四边形，得出AE=DF，AD=EF=2，证△AEB和△DFC全等得出BE=CF，求出CF=1，在Rt△DFC中，根据勾股定理求出即可．
解答：解：过A作AE⊥BC于E，
∵AE⊥BC，DF⊥BC，
∴∠AEB=∠DFC=90°，AE∥DF，
∵AD∥BC，
∴四边形AEFD是平行四边形，
∴AE=DF，AD=EF，
∵四边形ABCD是等腰梯形，AD∥BC，
∴∠B=∠C，
在△AEB和△DFC中
∵
，
∴△AEB≌△DFC，
∴CF=BE，
∵EF=AD=2，BC=4，
∴BE=CF=1，
在Rt△DFC中，由勾股定理得：CD=
=
=
，
故答案为：
．
∵AE⊥BC，DF⊥BC，
∴∠AEB=∠DFC=90°，AE∥DF，
∵AD∥BC，
∴四边形AEFD是平行四边形，
∴AE=DF，AD=EF，
∵四边形ABCD是等腰梯形，AD∥BC，
∴∠B=∠C，
在△AEB和△DFC中
∵
|
∴△AEB≌△DFC，
∴CF=BE，
∵EF=AD=2，BC=4，
∴BE=CF=1，
在Rt△DFC中，由勾股定理得：CD=
| DF2+CF2 |
| 22+12 |
| 5 |
故答案为：
| 5 |
点评：本题考查了等腰梯形的性质，勾股定理，平行四边形的性质和判定，全等三角形的性质和判定，解此题的关键是把等腰梯形转化成直角三角形和平行四边形，题目具有一定的代表性，是一道比较好的题目．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
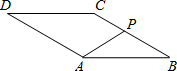（2012•营口）如图，菱形ABCD的边长为2，∠B=30°．动点P从点B出发，沿B-C-D的路线向点D运动．设△ABP的面积为y（B、P两点重合时，△ABP的面积可以看做0），点P运动的路程为x，则y与x之间函数关系的图象大致为（ ）
（2012•营口）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，-1）、B（-1，1）、C（0，-2）．
（2012•营口）如图，实线部分为某月牙形公园的轮廓示意图，它可看作是由⊙P上的一段优弧和⊙Q上的一段劣弧围成，⊙P与⊙Q的半径都是2km，点P在⊙Q上．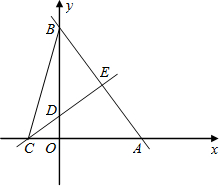
（2012•营口）如图，直线