题目内容
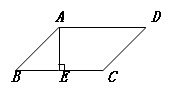
如图,在□ABCD中,AE⊥BC于E,AE=EB=EC=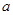 ,且
,且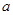 是一元二次方程
是一元二次方程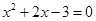 的根,则□ABCD的周长为( )
的根,则□ABCD的周长为( )
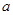 ,且
,且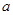 是一元二次方程
是一元二次方程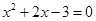 的根,则□ABCD的周长为( )
的根,则□ABCD的周长为( )
A. | B. |
C. | D. 或 或 |
A
试题分析:根据平行四边形的性质结合AE⊥BC可得AE=EB=EC=a,即可得到△AEB是等腰直角三角形,由勾股定理可求得AB、BC的长,解一元二次方程
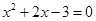 即可求得a的值,从而求得结果.
即可求得a的值,从而求得结果.∵平行四边形ABCD
∴AD∥BC,
∵AE⊥BC于E,
∵AE=EB=EC=a,
∴△AEB是等腰直角三角形,由勾股定理得:AB2=AE2+BE2,即AB=
 a,BC=BE+CE=2a,
a,BC=BE+CE=2a,∴平行四边形ABCD的周长=2(AB+BC)=2a(2+
 ),
),∵a是一元二次方程
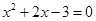 的根,解此方程得x=-3或x=1,显然x=-3,不合题意,x=1,
的根,解此方程得x=-3或x=1,显然x=-3,不合题意,x=1,∴x=a=1,
∴平行四边形ABCD的周长=2(AB+BC)=2a(2+
 )=2(2+
)=2(2+ )=4+2
)=4+2
故选A.
点评:本题要求我们能根据所给的条件与图形,观察出△BAE的特殊性,综合运用平行四边形的性质,勾股定理求得平行四边形的周长.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 中,
中, 4,
4,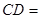 13,
13, 12,∠
12,∠
 90°,∠
90°,∠ 135°, 四边形
135°, 四边形

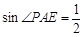 ③HP//AE ④HF=1 ⑤
③HP//AE ④HF=1 ⑤

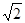 CH.
CH.

 为1,按上述方法所作的正方形的面积依次为
为1,按上述方法所作的正方形的面积依次为 ,
, ,…..,
,….., (n为正整数),那么第8个正方形的面积
(n为正整数),那么第8个正方形的面积 =___________.
=___________.