题目内容
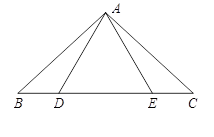
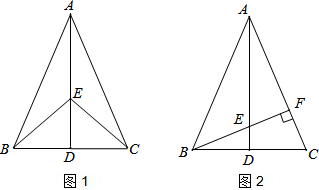
如图，点D，E在△ABC的边BC上，连 接AD，AE．①AB=AC；②AD=AE；③BD=CE．以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②?③：①③?②；②③?①．
（1）以上三个命题是真命题的为（直接作答） ；
（2）请选择一个真命题进行证明（先写出所选命题，然后证明）
（1）以上三个命题是真命题的为（直接作答） ；
（2）请选择一个真命题进行证明（先写出所选命题，然后证明）
（1）①②?③，①③?②，②③?①;（2）选择①③?②，证明见解析．
试题分析：（1）根据真命题的定义即可得出结论，
（2）根据全等三角形的判定方法及全等三角形的性质即可证明．
试题解析：（1）①②?③，①③?②，②③?①，
（2）选择①③?②，
证明：∵AB=AC，
∴∠B=∠C，
在△ABD和△ACE中，
∵
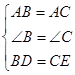
∴△ABD≌△ACE（SAS），
∴AD=AE．
练习册系列答案
相关题目
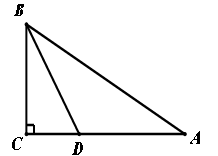
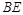平分∠A BC交CD于E，DF平分∠A DC交AB于F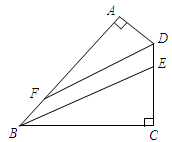
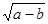+|a?3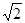
|＝0．C为AB的中点，P是线段AB上一动点，D是x轴正半轴上一点，且PO=PD，DE⊥AB于E．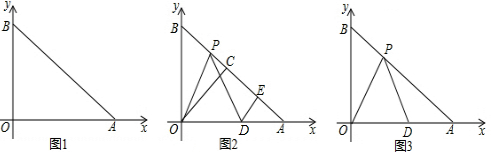
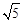.由此可知新正方形边长等于两个小正方形组成的矩形的对角线长．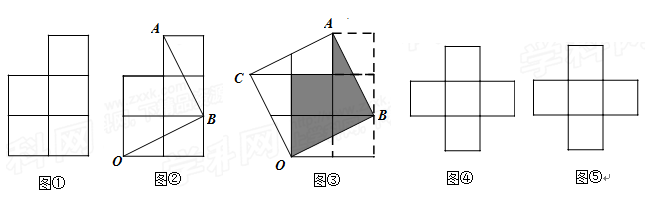
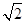)，C(1，0)， D为射线AO上一点，一动点P从A出发，运动路径为A→D→C，点P在AD上的运动速度是在CD上的3倍，要使整个运动时间最少，则点D的坐标应为（ ）
)
)
)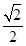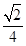