题目内容
【题目】设二次函数![]() ,一次函数
,一次函数![]() ,若方程
,若方程![]() 的两根是
的两根是![]() ,
,![]() .
.
(1)求b、c的值;
(2)当x满足![]() 时,比较
时,比较![]() 与x的大小并说明理由;
与x的大小并说明理由;
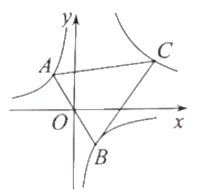
(3)设点M的坐标是![]() ,点P是抛物线
,点P是抛物线![]() 上的一个动点,当点P到点M的距离与到直线
上的一个动点,当点P到点M的距离与到直线![]() 的距离之和最小时,请直接写出点P坐标.
的距离之和最小时,请直接写出点P坐标.
【答案】(1)b=0,c=![]() ;(2)y1<x,理由见解析;(3)(2,2)
;(2)y1<x,理由见解析;(3)(2,2)
【解析】
(1)先把点(1,1),(2,2)的坐标分别代入抛物线解析式得到b,c的方程组,解方程组求出b,c的值即可;
(2)由于y1-x=![]() ,由1<x<2可得y1-x<0,从而求解;
,由1<x<2可得y1-x<0,从而求解;
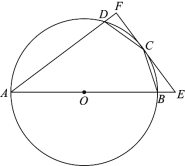
(3)先根据勾股定理及其逆定理证明△OP2M是直角三角形,然后可证P在直线与抛物线两交点之间的P2处时,点P到点M的距离与到直线![]() 的距离之和最小.
的距离之和最小.
解:(1)∵方程![]() 的两根是
的两根是![]() ,
,![]() ,
,
∴两交点坐标为(1,1),(2,2),
∴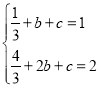 ,
,
解得b=0,c=![]() ;
;
(2)y1-x=![]() ,
,
当1<x<2时,y1-x<0,
所以y1<x;
(3)由题知,抛物线与直线的两个交点坐标为P1(1,1)、P2(2,2),
∵OM=4,OP2=![]() , MP2=
, MP2=![]() ,
,
∴OP22+MP22=OM2,
∴△OP2M是直角三角形,
∴∠OP2M=90°,
∴MP2⊥直线y2=x,
∴MP2到直线y2=x的距离最短,
又∵P到y2=x的距离是0,
∴当P点坐标是(2,2)时,P到M的距离与到直线y2=x距离之和最小,
即所求P点坐标是(2,2).

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.