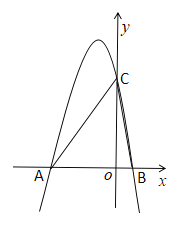题目内容
【题目】如图，在平面直角坐标系中，O为坐标原点，△ABC 的顶点 A (-2,0),点 B，C分别在x轴和y轴的正半轴上,∠ACB=90°,∠BAC=60°
(1)求点 B 的坐标;
(2)点 P 为 AC延长线上一点，过 P 作PQ∥x轴交 BC 的延长线于点 Q ,若点 P 的横坐标为t，线段PQ的长为d，请用含t的式子表示d;
(3) 在（2）的条件下，当PA=
d时，E是线段CQ上一点，连接OE，BP，若OE=BP，求∠APB-∠OEB的度数．.
【答案】（1）B（6，0）；（2）d=4t；（3）∠APB-∠OEB=30°．
【解析】
（1）在三角形AOC中，利用30度所对的直角边等于斜边的一半求出AC的长，在直角三角形ABC中，利用30度所对的直角边等于斜边的一半求出AB的长，由AB-OA求出OB的长，即可确定出B的坐标；
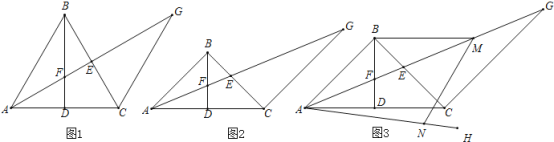
（2）如图1所示，在直角三角形MCP中，利用30度所对的直角边等于斜边的一半，由MP=t，表示出PC，在直角三角形QPC中，利用30度所对的直角边等于斜边的一半表示出PQ，即可得出d与t的关系式；
（3）如图2所示，过E作GF⊥x轴，交x轴于点F，交PQ于点G，在直角三角形QCP中，利用30度所对的直角边等于斜边的一半表示出PC，由AP-PC表示出AC，根据已知AC的长求出d的值，确定出PC与PQ的长，在直角三角形PCB中，利用勾股定理求出PB的长，即为PE的长，设OF=GM=x，表示出GE，由GF-EG表示出EF，在直角三角形OEF中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出OF=PC，再由OE=PB，利用HL得到直角三角形OEF与直角三角形PCB全等，利用全等三角形的对应角相等得到∠EOF=∠APB，再利用外角性质即可求出∠APB-∠OEB的度数．
（1）在Rt△AOC中，OA=2，∠BAC=60°，
∴∠ACO=30°，即AC=2OA=4，
在Rt△ABC中，∠ABC=30°，
∴AB=2AC=8，即OB=AB-OA=8-2=6，
则B（6，0）；
（2）如图1所示，
在Rt△MCP中，MP=t，∠MCP=30°，
∴CP=2MP=2t，
在Rt△CQP中，∠CQP=30°，CP=2t，
∴PQ=4t，即d=4t；
（3）如图2所示，过E作GF⊥x轴，交x轴于点F，交PQ于点G，
在Rt△PQC中，∠CQP=30°，PQ=d，
∴CP=
PQ=d，
∵AP=
d，
∴AC=AP-CP=
d=4，即d=12，
∴PQ=12，PC=6，MP=3，QM=9，
在Rt△CBP中，CP=6，BC=4
，
∴PB=
，
∴OE=PB=2
，
在Rt△OEF中，设OF=GM=x，QG=9-x，
在Rt△QEG中，GE=
（9-x），
∵MC=3，OC=2
，
∴GF=OM=5，
∴EF=5-（9-x），
在Rt△OEF中，根据勾股定理得：x2+[5-（9-x）]2=（2）2，
解得：x=6，
∴OF=PC=6，
在Rt△OEF和Rt△PBC中，
，
∴Rt△OEF≌Rt△PBC（HL），
∴∠AOE=∠APB，
∵∠AOE=∠OEB+∠ABC=∠OEB+30°，即∠AOE-∠OEB=30°，
则∠APB-∠OEB=30°．
