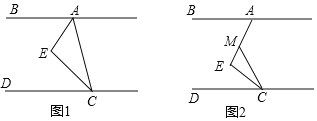Question

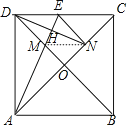
【题目】已知正方形中与交于点，点在线段上，作直线交直线于,过作于,设直线交于.

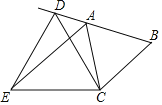
（1）如图，当在线段上时，求证：；

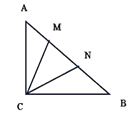
（2）如图2，当在线段上，连接,当时，求证：；

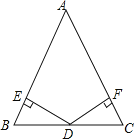
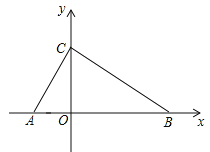
（3）在图3，当在线段上，连接,当时，求证：.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）证明见解析.

【解析】（1）先判断出OD=OA，∠AOM=∠DON，再利用同角的余角相等判断出∠ODN=∠OAM，判断出△DON≌△AOM即可得出结论；

（2）先判断出四边形DENM是菱形，进而判断出∠BDN=22.5°，即可判断出∠AMB=67.5°，即可得出结论；

（3）设CE=a，进而表示出EN=CE=a，CN=a，设DE=b，进而表示AD=a+b，根据勾股定理得，AC=（a+b），同（1）的方法得，∠OAM=∠ODN，得出∠EDN=∠DAE，进而判断出△DEN∽△ADE，得出，进而得出a=b，即可表示出CN=b，AC=b，AN=AC﹣CN=b，即可得出结论．

（1）∵正方形ABCD的对角线AC，BD相交于O，

∴OD=OA，∠AOM=∠DON=90°，

∴∠OND+∠ODN=90°，

∵∠ANH=∠OND，

∴∠ANH+∠ODN=90°，

∵DH⊥AE，

∴∠DHM=90°，

∴∠ANH+∠OAM=90°，

∴∠ODN=∠OAM，

∴△DON≌△AOM，

∴OM=ON；

（2）连接MN，

∵EN∥BD，

∴∠ENC=∠DOC=90°，∠NEC=∠BDC=45°=∠ACD，

∴EN=CN，同（1）的方法得，OM=ON，

∵OD=OD，

∴DM=CN=EN，

∵EN∥DM，

∴四边形DENM是平行四边形，

∵DN⊥AE，

∴DENM是菱形，

∴DE=EN，

∴∠EDN=∠END，

∵EN∥BD，

∴∠END=∠BDN，

∴∠EDN=∠BDN，

∵∠BDC=45°，

∴∠BDN=22.5°，

∵∠AHD=90°，

∴∠AMB=∠DME=90°﹣∠BDN=67.5°，

∵∠ABM=45°，

∴∠BAM=67.5°=∠AMB，

∴BM=AB；

（3）设CE=a（a＞0）

∵EN⊥CD，

∴∠CEN=90°，

∵∠ACD=45°，

∴∠CNE=45°=∠ACD，

∴EN=CE=a，

∴CN=a，

设DE=b（b＞0），

∴AD=CD=DE+CE=a+b，

根据勾股定理得，AC=AD=（a+b），

同（1）的方法得，∠OAM=∠ODN，

∵∠OAD=∠ODC=45°，

∴∠EDN=∠DAE，∵∠DEN=∠ADE=90°，

∴△DEN∽△ADE，

∴，

∴，

∴a=b（已舍去不符合题意的）

∴CN=a=b，AC=（a+b）=b，

∴AN=AC﹣CN=b，

∴AN2=2b2，ACCN=bb=2b2

∴AN2=ACCN．