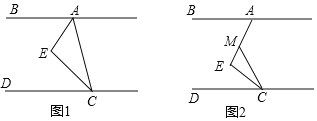题目内容
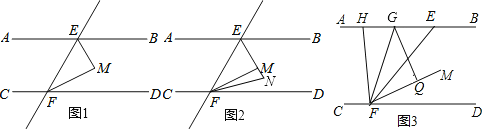
【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
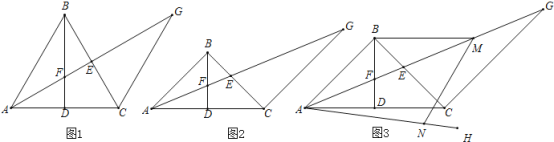
(1)如图1,若∠ABC=60°,求证:AF=![]() EG;
EG;
(2)如图2,若∠ABC=90°,求证:AF=![]() EG;
EG;
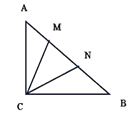
(3)在(2)的条件下如图3,过点A作∠CAH=![]() ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,![]() ,求BN的长.
,求BN的长.
【答案】(1)证明见解析;(2)证明见解析;(3)6.
【解析】
(1)先判断出△ABC是等边三角形,设DF=a,表示出AF、EF,根据两直线平行,内错角相等求出∠G=∠CAE=30°,表示出GE,然后相比即可;
(2)取EG的中点P,连接CF、CP,根据角平分线的定义求出∠BAE=∠FAC=22.5°,根据等腰直角三角形的对称性可得AF=CF,然后求出∠CFP=45°,再求出∠ECG=90°,根据直角三角形斜边上的中线等于斜边的一半可得CP=GP=![]() EG,根据两直线平行,内错角相等可得∠G=∠BAE=22.5°,再求出∠CPF=45°,根据等角对等边可得CF=CP,从而得到AF=CP,AF=
EG,根据两直线平行,内错角相等可得∠G=∠BAE=22.5°,再求出∠CPF=45°,根据等角对等边可得CF=CP,从而得到AF=CP,AF=![]() EG,整理即可得证;
EG,整理即可得证;
(3)过点B作BK⊥AM于K,过点M作ML⊥AH于H,先求出∠EAH=30°,根据直角三角形两锐角互余求出∠AML=∠BMN=60°,然后求出∠BMK=∠NML,再求出∠BAE=∠BME=22.5°,根据等角对等边可得AB=BM,根据等腰三角形三线合一的性质可得MK=![]() AM,根据直角三角形斜边上的中线等于斜边的一半可得ML=
AM,根据直角三角形斜边上的中线等于斜边的一半可得ML=![]() AM,从而得到MK=ML,再利用“角边角”证明△BMK和△NML全等,根据全等三角形对应边相等可得MN=BM,再根据等腰直角三角形的面积求出AB,再判断出△BMN是等边三角形,然后求解即可.
AM,从而得到MK=ML,再利用“角边角”证明△BMK和△NML全等,根据全等三角形对应边相等可得MN=BM,再根据等腰直角三角形的面积求出AB,再判断出△BMN是等边三角形,然后求解即可.
(1)证明:∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
设DF=a,
∵BD为△ABC的中线,AE为△ABC的角平分线,
∴AF=2a,EF=a,
∵CG∥AB,
∴∠G=∠CAE=∠CAE=30°,
∴GE=AE=AF+EF=2a+a=3a,
∴AF=![]() EG;
EG;
(2)证明:取EG的中点P,连接CF、CP,
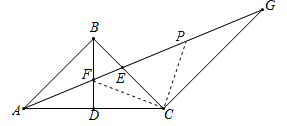
∵BA=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴AF=CF,
∵AF是△ABC的角平分线,
∴∠BAE=∠FAC=22.5°,
∴∠CFP=45°,
∵CG∥AB,
∴∠ECG=∠ABC=90°,
∴CP=GP=![]() EG,
EG,
∵CG∥AB,
∴∠G=∠BAE=22.5°,
∴∠CPF=45°,
∴CF=CP,
∴AF=![]() EG;
EG;
(3)过点B作BK⊥AM于K,过点M作ML⊥AH于H,
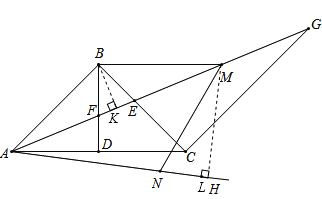
∵∠CAH=![]() ∠FAC,
∠FAC,
∴∠EAH=22.5°+![]() ×22.5°=30°,
×22.5°=30°,
∴∠AML=90°-30°=60°,
∵∠BMN与∠EAH互余,
∴∠BMN=90°-30°=60°,
∴∠BMK=∠NML,
∵AE是△ABC的平分线,CG∥AB,
∴∠BAE=∠BME=![]() ×45°=22.5°,
×45°=22.5°,
∴AB=BM,
∴MK=![]() AM,
AM,
∵∠MAH=30°,ML⊥AH,
∴MH=![]() AM,
AM,
∴MK=ML,
在△BMK和△NML中,
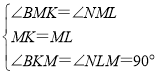 ,
,
∴△BMK≌△NML(ASA),
∴MN=BM,
∴MN=AB,
∵△ABC的面积为18,
∴![]() AB2=18,
AB2=18,
∴AB=6,
∵∠BMN=60°,BM=MN,
∴△BMN是等边三角形,
∴BN=MN=6.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案