题目内容
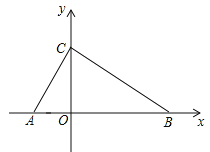
【题目】如图,已知抛物线y=ax2+bx+6(a≠0)与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.
(1)求抛物线y的函数表达式及点C的坐标;
(2)点M为坐标平面内一点,若MA=MB=MC,求点M的坐标;
(3)在抛物线上是否存在点E,使![]() ∠ABE=
∠ABE=![]() ∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
【答案】(1)y=-2x2-4x+6;(2)M(-1,![]() );(3)E1(-2,6),E2(-4,-10) .
);(3)E1(-2,6),E2(-4,-10) .
【解析】(1)根据抛物线过A、B两点,待定系数法求解可得;;
(2)由(1)知抛物线对称轴为直线x=-1,设H为AC的中点,求出直线AC的垂直平分线的解析式即可得解;
(3)①过点A作![]() 交y轴于点F,交CB的延长线于点D,证明ΔAOF∽ΔCOA,求得
交y轴于点F,交CB的延长线于点D,证明ΔAOF∽ΔCOA,求得![]() ,分别求出直线AF、BC的解析式的交点
,分别求出直线AF、BC的解析式的交点![]() ,求出
,求出![]() ,
,
根据![]() ∠ABE=
∠ABE=![]() ∠ACB求出
∠ACB求出![]() ∠ABE=2,易求E点坐标.
∠ABE=2,易求E点坐标.
(1)把A(-3,0)、B(1,0)代入y=ax2+bx+6得,
![]() ,解得
,解得![]()
∴y=-2x2-4x+6,
令x=0,则y=6,
∴C(0,6);
(2)![]() =-2(x+1)2+8,
=-2(x+1)2+8,
∴抛物线的对称轴为直线x=-1.
设H为线段AC的中点,故H(![]() ,3).
,3).
设直线AC的解析式为:y=kx+m,则有
![]() ,解得,
,解得,![]() ,
,
∴y=2x+6
设过H点与AC垂直的直线解析式为:![]() ,
,
∴![]()
∴b=![]()
∴![]()
∴当x=-1时,y=![]()
∴M(-1,![]() )
)
(3)①过点A作![]() 交y轴于点F,交CB的延长线于点D
交y轴于点F,交CB的延长线于点D
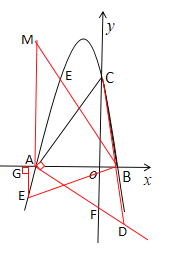
∵∠ACO+∠CAO=90°,∠DAO+∠CAO=90°
∴∠DAO=∠ACO
∵∠ACO=∠ACO
∴ΔAOF∽ΔCOA
∴![]()
∴![]()
∵OA=3,OC=6
∴![]()
∴![]()
直线AF的解析式为:![]()
直线BC的解析式为:![]()
∴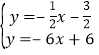 ,解得
,解得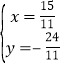
∴![]()
∴![]()
∴![]() ∠ACB=
∠ACB=![]()
∵![]() ∠ABE=
∠ABE=![]() ∠ACB
∠ACB
∴![]() ∠ABE=2
∠ABE=2
过点A作![]() 轴,连接BM交抛物线于点E
轴,连接BM交抛物线于点E
∵AB=4,![]() ∠ABE=2
∠ABE=2
∴AM=8
∴M(-3,8)
直线BM的解析式为:![]()
∴![]() ,解得
,解得![]()
∴y=6
∴E(-2,6)
②当点E在x轴下方时,过点E作![]() ,连接BE,设点E
,连接BE,设点E![]()
∴![]() ∠ABE=
∠ABE=![]() 2
2
∴m=-4或m=1(舍去)
可得E(-4,-10)
综上所述E1(-2,6),E2(-4,-10)