题目内容
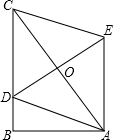
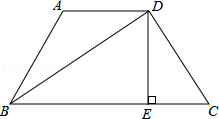
(8分)如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F.

(1)试说明:AF=FC;
(2)如果AB=3,BC=4,求AF的长.

(1)试说明:AF=FC;
(2)如果AB=3,BC=4,求AF的长.
(1)详见解析;(2)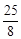 .
.
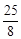 .
.试题分析:(1)观察图形,可得AE=DC,又∵∠FEA=∠DFC,∠AEF=∠CDF,由全等三角形判定方法证△AEF≌△CDF,即得EF=DF,从而得到AF=FC.(2)在Rt△CDF中应用勾股定理即可得.
试题解析:(1)证明:由矩形性质可知,AE=AB=DC,
根据对顶角相等得,∠EFA=∠DFC,
而∠E=∠D=90°,
∴由AAS可得,△AEF≌△CDF。∴AF=FC.
(2)设FA=x,则FC=x,FD=
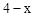 ,
,在Rt△CDF中,CF2=CD2+DF2,即
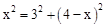 ,解得x=
,解得x=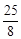 .
.考点: 1.翻折变换(折叠问题);2.矩形的性质;3.全等三角形的判定与性质;4勾股定理.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题: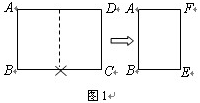



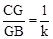 ,则
,则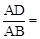 (用含k的代数式表示).
(用含k的代数式表示).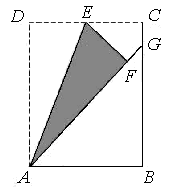
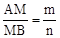 ,则有结论:
,则有结论: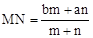 。
。
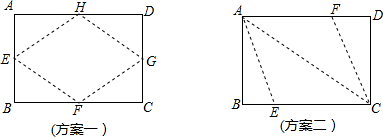
 ADCE中,DE最小的值是
ADCE中,DE最小的值是