题目内容
动手操作:在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小明同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).
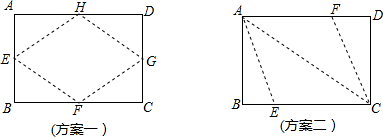
(1)你能说出小颖、小明所折出的菱形的理由吗?
(2)请你通过计算,比较小颖和小明同学的折法中,哪种菱形面积较大?

(1)你能说出小颖、小明所折出的菱形的理由吗?
(2)请你通过计算,比较小颖和小明同学的折法中,哪种菱形面积较大?
(1)理由见解析;(2)小明同学所折的菱形面积较大.
试题分析:(1)要证所折图形是菱形,只需证四边相等即可.(2)按照图形用面积公式计算S1=30和S2=35.21,可知方案二小明同学所折的菱形面积较大.
试题解析:(1)小颖的理由:依次连接矩形各边的中点所得到的四边形是菱形.
小明的理由:∵ABCD是矩形,
∴AD∥BC. ∴∠DAC=∠ACB.
又∵∠CAE=∠CAD,∠ACF=∠ACB,
∴∠CAE=∠CAD=∠ACF=∠ACB. ∴AE="EC=CF=FA." ∴四边形AECF是菱形.
(2)方案一:
 .
.方案二:设BE=x,则
 ,
,∴
 .
.由AECF是菱形,得AE2=CE2,∴
 ,解得
,解得 .
.∴
 .
.∵

∴方案二小明同学所折的菱形面积较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目