题目内容
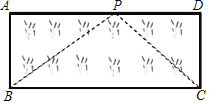
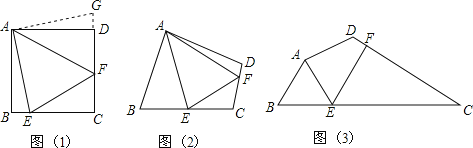
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
(发现证明)小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
(类比引申)如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
(探究应用)如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,∠EAF=75°且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】【发现证明】见解析;【类比引申】∠BAD=2∠EAF. 【探究应用】这条道路EF的长约为109米.
【解析】
[发现证明]根据旋转的性质可以得到△ADG≌△ABE,则GF=BE+DF,只要再证明△AFG≌△AFE即可.
[类比引申]延长CB至M,使BM=DF,连接AM,证△ADF≌△ABM,证△FAE≌△MAE,即可得出答案;
[探究应用]利用等边三角形的判定与性质得到△ABE是等边三角形,则BE=AB=80米.把△ABE绕点A逆时针旋转150°至△ADG,只要再证明∠BAD=2∠EAF即可得出EF=BE+FD.
[发现证明]根据旋转的性质可以得到△ADG≌△ABE,则GF=BE+DF,只要再证明△AFG≌△AFE即可.
[类比引申]∠BAD=2∠EAF.如图(2),延长CB至M,使BM=DF,连接AM,
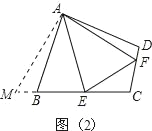
证△ADF≌△ABM,证△FAE≌△MAE,即可得出答案;
[探究应用]如图3,把△ABE绕点A逆时针旋转150°至△ADG,连接AF.
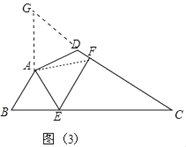
∵∠BAD=150°,∠DAE=90°,
∴∠BAE=60°.
又∵∠B=60°,
∴△ABE是等边三角形,
∴BE=AB=80米.
根据旋转的性质得到:∠ADG=∠B=60°,
又∵∠ADF=120°,
∴∠GDF=180°,即点G在CD的延长线上.
易得,△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAG=∠BAD=150°,∠FAE=75°
∴∠GAF=∠FAE,
在△GAF和△FAE中,
AG=AE,∠GAF=∠FAE,AF=AF,
∴△AFG≌△AFE(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴EF=BE+DF=80+40(![]() ﹣1)≈109(米),
﹣1)≈109(米),
即这条道路EF的长约为109米.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案