题目内容

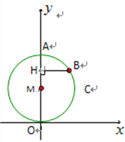
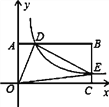
【题目】如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数（x＞0）与AB相交于点D，与BC相交于点E，若BD=3AD，且△ODE的面积是12，则k=（　　）

A. 6 B. 9 C. D.

【答案】D

【解析】分析：所给的三角形面积等于长方形面积减去三个直角三角形的面积，然后即可求出B的横纵坐标的积即是反比例函数的比例系数．

详解：∵四边形OCBA是矩形，

∴AB=OC，OA=BC，

设B点的坐标为（a，b），

∵BD=3AD，

∴D（，b），

∵点D，E在反比例函数的图象上，

∴=k，

∴ab=4k，

∴E（a，），

∵S△ODE=S矩形OCBA-S△AOD-S△OCE-S△BDE=ab--k-（b-）=12，

∴k=，

故选：D．

练习册系列答案
相关题目

【题目】问题：如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，试判断BE、EF、FD之间的数量关系．

（发现证明）小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF＝BE+FD，请你利用图（1）证明上述结论．

（类比引申）如图（2），四边形ABCD中，∠BAD≠90°，AB＝AD，∠B+∠D＝180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足　 　关系时，仍有EF＝BE+FD．

（探究应用）如图（3），在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB＝AD＝80米，∠B＝60°，∠ADC＝120°，∠BAD＝150°，道路BC、CD上分别有景点E、F，∠EAF＝75°且AE⊥AD，DF＝40（﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：≈1.41，≈1.73）

【题目】如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.

（1）求∠C的度数;

（2）已知DF的长是关于的方程--6=0的一个根,求该方程的另一个根.

【题目】在□ABCD，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF.

（1）求证：四边形BFDE是矩形；

（2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB.

【题目】如图8,在平面直角坐标系中,点A坐标为（0,3）,点B（,）是以OA为直径的⊙M上的一点,且tan∠AOB=,BH⊥轴,H为垂足,点C（,）.

（1）求H点的坐标;

（2）求直线BC的解析式;

（3）直线BC是否与⊙M相切?请说明理由.

【题目】已知反比例函数y=的图象与一次函数y=kx+m的图象相交于点A（2，1）．

（1）分别求出这两个函数的解析式；

（2）当x取什么范围时，反比例函数值大于0；

（3）若一次函数与反比例函数另一交点为B，且纵坐标为﹣4，当x取什么范围时，反比例函数值大于一次函数的值；

（4）试判断点P（﹣1，5）关于x轴的对称点P′是否在一次函数y=kx+m的图象上．

【题目】中国古代有着辉煌的数学成就，《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.

（1）小聪想从这4部数学名著中随机选择1部阅读，求他选中《九章算术》的概率；

（2）小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容，用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.

【题目】反比例函数（a>0,a为常数）和在第一象限内的图象如图所示，点M在的图象上，MC丄x轴于点C，交的图象于点A，MD丄y轴于点D，交的图象于点B，当点M在的图象上运动时，以下结论：

①S△CDB=S△CCA

②四边形OAMB的面积为2-a

③当a=l时，点A是MC的中点

④若S四边形OAMB+S△CDB，则四边形OCMD为正方形.其中正确是________（把所有正确结论的序号写在横线上)

【题目】把下列各数填在相应的大括号里

，，，，，，，，，，

正数集合{　 …}

非负整数集合{ 　…}

负分数集合{ 　…}

有理数集合{ …}．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网