��Ŀ����
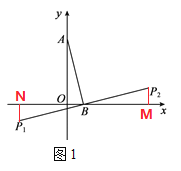
����Ŀ����ƽ��ֱ������ϵxOy�У���A������Ϊ(0��m)����m��0����B������Ϊ(n��0)�����߶�AB�Ƶ�B��ת90�����ֱ�õ��߶�B P1��B P2���Ƶ�P1��P2Ϊ��A���ڵ�B�������������ͼ1Ϊ��A���ڵ�B�������������ʾ��ͼ��
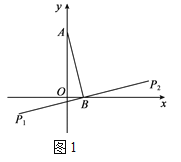
(1)��֪��A(0��4)��
�ٵ���B������ֱ�Ϊ(1��0)��(-2��0)ʱ����A���ڵ�B�����������������ֱ�Ϊ ��
�ڵ㣨x��y���ǵ�A���ڵ�B�������������ֱ��д��y��x֮��Ĺ�ϵʽ��
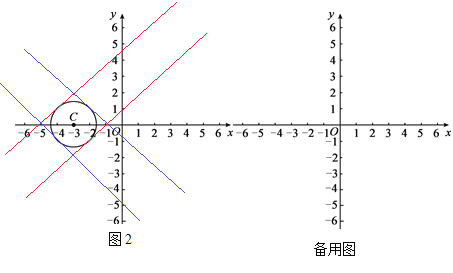
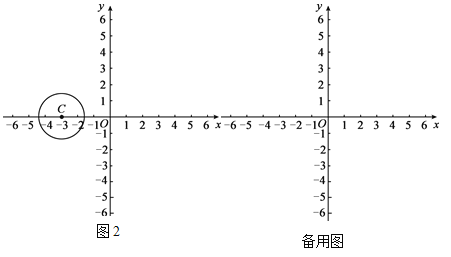
(2)��ͼ2����C������Ϊ(-3��0)����CΪԲ�ģ� ![]() Ϊ�뾶��Բ�����ڡ�C�ϴ��ڵ�A���ڵ�B�������������ֱ��д����A��������m��ȡֵ��Χ��
Ϊ�뾶��Բ�����ڡ�C�ϴ��ڵ�A���ڵ�B�������������ֱ��д����A��������m��ȡֵ��Χ��
���𰸡���1���٣�-3��-1������5��1������-6��2������2��-2������y=x-4��y=-x-4.
��2��-5��m��-1��1��m��5
�����������������(1)����![]() ��x���ڵ�M����
��x���ڵ�M����![]() ��x���ڵ�N��������֪������֤
��x���ڵ�N��������֪������֤![]() ��
��![]() ��
��![]() ������ȫ�������ε����ʿɵ�
������ȫ�������ε����ʿɵ�![]() =OB=
=OB= ![]() ��OA=BM=BN������A(0��4)������B������Ϊ(1��0)ʱ��������õ�A���ڵ�B�ġ�����㡱������ֱ�Ϊ��-3��-1������5��1��������A(0��4)������B������Ϊ(-2��0)ʱ��������õ�A���ڵ�B�ġ�����㡱������ֱ�Ϊ��-6��2������2��-2�������ɢٿ�֪��x=y+4��-x-y=4�����ɵ�y��x֮��Ĺ�ϵʽΪy=x-4��y=-x-4����2�����A������Ϊ��0��m�����㣨x��y���ǵ�A���ڵ�B�ġ�����㡱���ɣ�1���ķ����ɵ�y=x-m��y=-x-m����ֱ��y=x-m����ʱ����ͼ��ͼ�еĺ��ߣ�������ֱ��y=x-m��x�ᡢy����Χ�ɵ�������Ϊ����ֱ�������Ρ����ߵ����ʡ����ɶ��������m=1����m=5�����ɵ�1��m��5����ֱ��y=-x-m����ʱ����ͼ��ͼ�е����ߣ���ͬ���ɵ�-5��m��-1�����Ե�A��������m��ȡֵ��ΧΪ-5��m��-1��1��m��5.
��OA=BM=BN������A(0��4)������B������Ϊ(1��0)ʱ��������õ�A���ڵ�B�ġ�����㡱������ֱ�Ϊ��-3��-1������5��1��������A(0��4)������B������Ϊ(-2��0)ʱ��������õ�A���ڵ�B�ġ�����㡱������ֱ�Ϊ��-6��2������2��-2�������ɢٿ�֪��x=y+4��-x-y=4�����ɵ�y��x֮��Ĺ�ϵʽΪy=x-4��y=-x-4����2�����A������Ϊ��0��m�����㣨x��y���ǵ�A���ڵ�B�ġ�����㡱���ɣ�1���ķ����ɵ�y=x-m��y=-x-m����ֱ��y=x-m����ʱ����ͼ��ͼ�еĺ��ߣ�������ֱ��y=x-m��x�ᡢy����Χ�ɵ�������Ϊ����ֱ�������Ρ����ߵ����ʡ����ɶ��������m=1����m=5�����ɵ�1��m��5����ֱ��y=-x-m����ʱ����ͼ��ͼ�е����ߣ���ͬ���ɵ�-5��m��-1�����Ե�A��������m��ȡֵ��ΧΪ-5��m��-1��1��m��5.
���������
��1���٣�-3��-1������5��1������-6��2������2��-2��.
��y=x-4��y=-x-4.
��2��-5��m��-1��1��m��5