ЬтФПФкШн
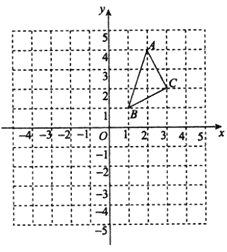
ЁОЬтФПЁПдФЖСВФСЯЃКИїРрЗНГЬЕФНтЗЈЃКЧѓНтвЛдЊвЛДЮЗНГЬЃЌИљОнЕШЪНЕФЛљБОаджЪЃЌАбЗНГЬзЊЛЏЮЊx=aЕФаЮЪН.ЧѓНтЖўдЊвЛДЮЗНГЬзщЃЌАбЫќзЊЛЏЮЊвЛдЊвЛДЮЗНГЬРДНтЃЛРрЫЦЕФЃЌЧѓНтШ§дЊвЛДЮЗНГЬзщЃЌАбЫќзЊЛЏЮЊНтЖўдЊвЛДЮЗНГЬзщ.ЧѓНтвЛдЊЖўДЮЗНГЬЃЌАбЫќзЊЛЏЮЊСНИівЛдЊвЛДЮЗНГЬРДНт.ЧѓНтЗжЪНЗНГЬЃЌАбЫќзЊЛЏЮЊећЪНЗНГЬРДНтЃЌгЩгкЁАШЅЗжФИЁБПЩФмВњЩњдіИљЃЌЫљвдНтЗжЪНЗНГЬБиаыМьбщ.ИїРрЗНГЬЕФНтЗЈВЛОЁЯрЭЌЃЌЕЋЪЧЫќУЧгавЛИіЙВЭЌЕФЛљБОЪ§бЇЫМЯызЊЛЏЃЌАбЮДжЊзЊЛЏЮЊвбжЊ.гУЁАзЊЛЏЁБЕФЪ§бЇЫМЯыЃЌЮвУЧЛЙПЩвдНтвЛаЉаТЕФЗНГЬ.Р§ШчЃЌвЛдЊШ§ДЮЗНГЬ![]() ЃЌПЩвдЭЈЙ§вђЪНЗжНтАбЫќзЊЛЏЮЊ
ЃЌПЩвдЭЈЙ§вђЪНЗжНтАбЫќзЊЛЏЮЊ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌЫљвдx=0Лђx+2=0Лђx-1=0ЃЌЫљвдЗНГЬЃК
ЃЌЫљвдx=0Лђx+2=0Лђx-1=0ЃЌЫљвдЗНГЬЃК![]() ЕФНтЪЧx1=0ЃЌx2=-2ЃЌx3=1ЃЛ
ЕФНтЪЧx1=0ЃЌx2=-2ЃЌx3=1ЃЛ
ЃЈ1ЃЉЮЪЬтЃКгУЁАзЊЛЏЁБЫМЯыЧѓЗНГЬ![]() ЕФНт
ЕФНт
ЃЈ2ЃЉгІгУЃКШчЭМЃЌвбжЊОиаЮВнЦКABCDЕФГЄAD=8mЃЌПэAB=3mЃЌаЁЛЊАбвЛИљГЄЮЊ10mЕФЩўзгЕФвЛЖЫЙЬЖЈдкЕуBЃЌбиВнЦКБпбиBAЃЌADзпЕНЕуPДІЃЌАбГЄЩўPBЖЮРжБВЂЙЬЖЈдкЕуPЃЌШЛКѓбиВнЦКБпбиPDЁЂDCзпЕНЕуCДІЃЌАбГЄЩўЪЃЯТЕФвЛЖЮРжБЃЌГЄЩўЕФСэвЛЖЫЧЁКУТфдкЕуC.ЧѓAPЕФГЄ.
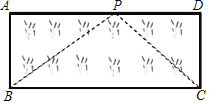
ЁОД№АИЁПЃЈ1ЃЉ3ЃЛЃЈ2ЃЉAP=4mЃЎ
ЁОНтЮіЁП
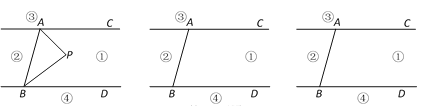
ЃЈ1ЃЉСНБпЦНЗНЃЌАбЮоРэЗНГЬзЊЛЏЮЊећЪНЗНГЬЃЌЧѓНтЃЌзЂвтбщИљЃЛ
ЃЈ2ЃЉЩшAPЕФГЄЮЊxmЃЌИљОнЙДЙЩЖЈРэКЭBP+CP=10ЃЌПЩСаГіЗНГЬЃЌгЩгкЗНГЬКЌгаИљКХЃЌСНБпЦНЗНЃЌАбЮоРэЗНГЬзЊЛЏЮЊећЪНЗНГЬЃЌЧѓНтЃЌ
НтЃКЃЈ1ЃЉ![]()
ЗНГЬЕФСНБпЦНЗНЃЌЕУ2x+3=x2ЃЌ
НтЕУx1=-1ЃЈЩсШЅЃЉЃЌx2=3ЃЌ
ЕБx=-1ЪБЃЌ![]() =
=![]() =1Ёй-1ЃЌ
=1Ёй-1ЃЌ
Ыљвд-1ВЛЪЧдЗНГЬЕФНтЃЎ
ЫљвдЗНГЬ![]() ЕФНтЪЧx=3ЃЛ
ЕФНтЪЧx=3ЃЛ
ЃЈ2ЃЉЩшAP=xЃЌдђDP=8-xЃЌ
ЁпBP+CP=10ЃЌ
ИљОнЙДЙЩЖЈРэЃКBP=![]() ЃЌCP=
ЃЌCP=![]()
Ёр![]()
![]()
СНБпЦНЗНЃЌЕУ![]()
ећРэЃЌЕУ![]()
СНБпЦНЗНВЂећРэЃЌЕУx2-8x+16=0
МДЃЈx-4ЃЉ2=0
Ыљвдx=4ЃЎ
ОМьбщЃЌx=4ЪЧЗНГЬЕФНтЃЎ
Д№ЃКAPЕФГЄЮЊ4mЃЎ
ЙЪД№АИЮЊЃКЃЈ1ЃЉ3ЃЛЃЈ2ЃЉAP=4mЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ