题目内容
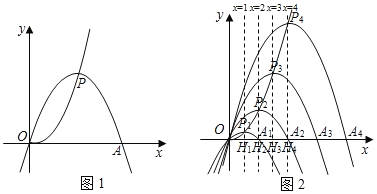
【题目】已知点P为抛物线y![]() x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
(1)①当△OPA为直角三角形时,m= ;
②当△OPA为等边三角形时,求此时“yp”的解析式;
(2)若P点的横坐标分别为1,2,3,…n(n为正整数)时,抛物线“yp”分别记作“![]() ”、“
”、“![]() ”…,“
”…,“![]() ”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
1)① Pn的坐标为 ;OAn= ;(用含n的代数式来表示)
②当PnHn﹣OAn=16时,求n的值.
2)是否存在这样的An,使得∠OP4An=90°,若存在,求n的值;若不存在,请说明理由.
【答案】(1)① 2;② y![]() x2+2
x2+2![]() x;(2)1):① (n,
x;(2)1):① (n,![]() n2);2n;② n=8;2):存在,n=10.
n2);2n;② n=8;2):存在,n=10.
【解析】
(1)①由△OPA为直角三角形时.得到△OPA为以点P为顶点的等腰直角三角形,从而可得答案,②由△OPA为等边三角形,过P作![]() 于
于![]() ,利用三角函数与抛物线的解析式
,利用三角函数与抛物线的解析式![]() ,求点
,求点![]() 的坐标,从而可得答案,
的坐标,从而可得答案,
(2)1)①利用Pn的横坐标为n,结合抛物线的对称性可得答案,②由 PnHn﹣OAn=16,建立方程求解即可,2) 画出图形,证明Rt△OP4H4∽Rt△P4AnH4即可得到答案.
解:(1)①当△OPA为直角三角形时.
∵PO=PA,故△OPA为以点P为顶点的等腰直角三角形,
∴点P的横坐标和纵坐标相同,故点P(m,m),
将点P的坐标代入y![]() x2得:m
x2得:m![]() m2,解得:m=0或2(舍去0).
m2,解得:m=0或2(舍去0).
故答案为:2;
②当△OPA为等边三角形时,如图,过P作![]() 于
于![]() ,
,
![]()
![]()
![]() P(m,
P(m,![]() m),
m),
将点P的坐标代入抛物线表达式![]() ,
,
解得:m=2![]() ,
,
故点P的坐标为(2![]() ,6),
,6),
故“yp”的解析式为:y=a(x﹣2![]() )2+6,
)2+6,
点A的坐标为(2m,0),即(4![]() ,0),
,0),
将点A的坐标代入y=a(x﹣2![]() )2+6并解得:a
)2+6并解得:a![]() ,
,
故“yp”的解析式为:y![]() (x﹣2
(x﹣2![]() )2+6
)2+6![]() x2+2
x2+2![]() x;
x;
(2)1)① 由题意得:Pn的横坐标为n,则其坐标为(n,![]() n2),
n2),
由抛物线的对称性得:An=2n.
故答案为:(n,![]() n2);2n;
n2);2n;
②由题意得:PnHn﹣OAn![]() n2﹣2n=16,
n2﹣2n=16,
解得:n=8或﹣4(舍去﹣4),
∴n=8;
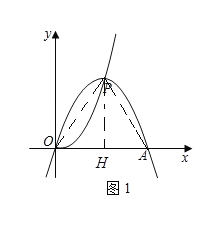
2)存在,理由:
如下图所示,由1)知,点P4的坐标为(4,8),An=2n,
即OH4=4,P4H4=8,H4An=2n﹣4,
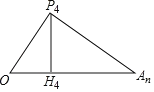
∵∠OP4An=90°,∴∠OP4H4+∠H4P4An=90°.
∵∠H4P4An+∠P4AnH4=90°,
∴∠OP4H4=∠P4AnH4,
∴Rt△OP4H4∽Rt△P4AnH4,
![]()
∴P4H42=OH4H4An,
即82=4×(2n﹣4),
解得:n=10.
![]() 当img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/03/d07c1de6/SYS202007220309563219592517_DA/SYS202007220309563219592517_DA.015.png" width="44" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />时,使得∠
当img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/03/d07c1de6/SYS202007220309563219592517_DA/SYS202007220309563219592517_DA.015.png" width="44" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />时,使得∠![]() =90°.
=90°.

 黄冈创优卷系列答案
黄冈创优卷系列答案