题目内容
【题目】有一块直角三角形的绿地,量得两直角边长分别为5m,12m.现在要将绿地扩充成等腰三角形绿地,且扩允部分是以12m为直角边的直角三角形,求扩充部分三角形绿地的面积.(如图备用)

【答案】扩充后等腰三角形绿地的面积是30m2或48m2或71.4m2.
【解析】
根据勾股定理求出斜边AB, (1) 当AB=AD时或AB=BD,求出CD即可; (2) 当AB=BD时,求出CD、AD,即可求出△ABD的面积; (3) 当DA=DB时,设AD=x,则CD=x-5,根据勾股定理,列出方程,求出x,即可求出△ABD的面积;
解:
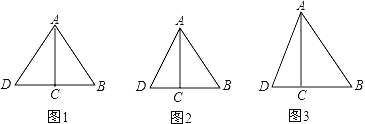
在Rt△ABC中,∵∠ACB=90°,AC=5m,BC=12m,
∴AB=13m,
(1)如图1,当AB=AD时,CD=5m,
则△ABD的面积为: ![]()
若延长AC到D,使CD=AC=12m,则△ABD的面积为![]()
60﹣30=30 (m2);
(2)图2,当AB=BD时,CD=8m,则△ABD的面积为:![]()
78﹣30=48(m2);
(3)如图3,当DA=DB时,设AD=x,则CD=x﹣5,
则![]() ,
,
∴x=16.9,
则△ABD的面积为: ![]()
101.4﹣30=71.4(m2);
答:扩充后等腰三角形绿地的面积是30m2或60m2或71.4m2.

练习册系列答案
相关题目