题目内容
【题目】如图,在△ABC中,∠BAC=90°,AB=5,AC=12,点D是BC的中点,将△ABD沿AD翻折得到△AED,连接BE,CE.则CE=___________。

【答案】![]()
【解析】
如图,连接BE交AD于O,作AH⊥BC于H.首先证明AD垂直平分线段BE,△BCE是直角三角形,求出BC、BE,在Rt△BCE中,利用勾股定理即可解决问题.
如图连接BE交AD于O,作AH⊥BC于H.
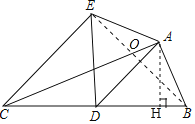
在Rt△ABC中,∵AC=12,AB=5,
∴BC=![]() =13,
=13,
∵CD=DB,
∴AD=DC=DB=6.5,
∵![]() BCAH=
BCAH=![]() ABAC,
ABAC,
∴AH=![]() ,
,
∵AE=AB,
∴点A在BE的垂直平分线上.
∵DE=DB=DC,
∴点D在BE的垂直平分线上,△BCE是直角三角形,
∴AD垂直平分线段BE,
∵![]() ADBO=
ADBO=![]() BDAH,
BDAH,
∴OB=![]() ,
,
∴BE=2OB=![]() ,
,
在Rt△BCE中,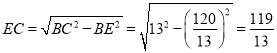 .
.
故答案为:![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目






