题目内容
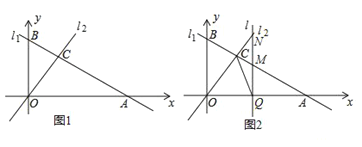
【题目】如图1,直线l1:![]() 与坐标轴分别交于点A,B,与直线l2:
与坐标轴分别交于点A,B,与直线l2:![]() 交于点C.
交于点C.
(1)求A,B两点的坐标;
(2)求△BOC的面积;
(3)如图2,若有一条垂直于x轴的直线l以每秒2个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.
①当OA=2MN时,求t的值;
②试探究是否存在点Q,使得以△OQC为等腰三角形?若存在,请直接写出t的值;若不存在,请说明理由
【答案】A(6,0),B(0,3);(2)△BOC的面积为3;(3)①t=1或t=3,②t=1,2,![]() ,
,![]()
【解析】
(1)令x=0得到y=3,令y=0,得到x=6,从而可得A、B点的坐标;
(2)构建方程组确定点C坐标即可解决问题;
(3)①根据绝对值方程即可解决问题;
②分为三种情况,画出图形,根据等腰三角形的性质求出即可.
(1)对于直线![]() ,令x=0得到y=3,令y=0,得到x=6,
,令x=0得到y=3,令y=0,得到x=6,
∴A(6,0),B(0,3).
(2)由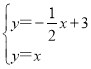 ,解得
,解得![]() ,
,
∴C(2,2),
∴S△OBC=![]() ×3×2=3
×3×2=3
(3)①设M(6-2t,-![]() (6-2t)+3),N(6-2t,6-2t),
(6-2t)+3),N(6-2t,6-2t),
∴MN=|-![]() (6-2t)+3-(6-2t)|=|3t-6|,
(6-2t)+3-(6-2t)|=|3t-6|,
∵OA=2MN,
∴6=2|3t-6|,
解得t=1或3;
②分三种情况:
i)、CO为底时,Q为顶点时,如图①,
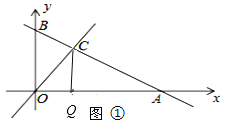
当∠COQ=45°,CQ=OQ,
∵C(2,2),
∴OQ=CQ=2,
∴AQ=OA-OQ=6-2=4,
∴t=4÷2=2(s);
ii)当CO为腰时,C为顶点时,如图②,过C作CM⊥OA于M,
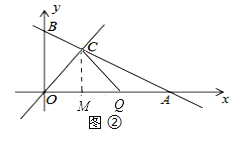
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴AQ=OA-OQ=2,
∴t=2÷2=1(s);
iii)当CO为腰时,O为顶点时,如图③:
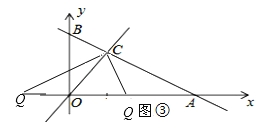
OQ=OC=2![]() ,
,
AQ=AO-OQ=6-2![]() 或AQ=AO+OQ=6+2
或AQ=AO+OQ=6+2![]() .
.
∴t=![]() 或t=
或t=![]() .
.
综上所述:t的值为1或2或![]() 或
或![]() .
.