题目内容
【题目】如图，点D在Rt△ABC的斜边AB上，且AC=6,
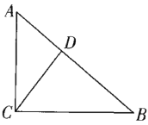
(1) 若AB比BC大2,①求AB的长；②若CD⊥AB于点D,求CD的长.
(2)若AD=7，DB=11， ∠CDB=2∠B，求CD的长.
【答案】（1）①10；②4.8；（2）9
【解析】
（1）①设AB=x,根据勾股定理列方程进行解答；②利用三角形的面积公式进行求解；（2）取AB的中点E，连接CE，根据直角三角形斜边上的中线等于斜边的一半可得CE=BE=
AB，根据等边对等角可得∠B=∠BCE，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CED=2∠B，从而得到∠CDB=∠CED，再根据等角对等边可得CD=CE．
解：（1）①设AB=x，则BC=x-2
在Rt△ABC中，
∴
解得：x=10
∴AB的长为10
②由①可知，BC=10-2=8
∵CD⊥AB
∴
∴
解得：CD=4.8
（2）解：如图，取AB的中点E，连接CE，
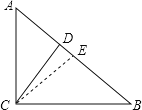
∵AD=7，DB=11，
∴AB=AD+DB=7+11=18，
∴CE=BE=AB=×18=9，
∴∠B=∠BCE，
由三角形的外角性质得，∠CED=∠B+∠BCE=2∠B，
∵∠CDB=2∠B，
∴∠CDB=∠CED，
∴CD=CE=9．
练习册系列答案
相关题目
