题目内容
【题目】(8分)如图,在ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,
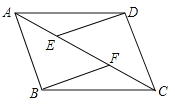
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
【答案】(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;(2)证明见试题解析.
【解析】
试题分析:(1)根据平行四边形的性质得出AB=CD,AD=CB,AB∥CD,AD∥CB,进一步得到∠BAF=∠DCE,∠DAE=∠BCF,由SSS证明△ABC≌△CDA;由SAS证明△ABF≌△CDE;由SAS证明△ADE≌△CBF(SAS);
(2)由△ABF≌△△CDE,得出∠AFB=∠CED,即可证出DE∥BF.
试题解析:(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;理由如下:
∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,AB∥CD,AD∥CB,∴∠BAF=∠DCE,∠DAE=∠BCF,在△ABC和△CDA中,∵AB=CD,CB=AD,AC=CA,∴△ABC≌△CDA(SSS);
∵AE=CF,∴AF=CE,在△ABF和△CDE中,∵AB=CD,∠BAF=∠DCE,AF=CE,∴△ABF≌△CDE(SAS);
在△ADE和△CBF中,∵AD=CB,∠DAE=∠BCF,AE=CF,∴△ADE≌△CBF(SAS).
(2)∵△ABF≌△△CDE,∴∠AFB=∠CED,∴DE∥BF.

练习册系列答案
相关题目
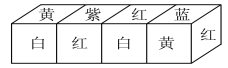
【题目】把正方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问长方体的下底面共有多少朵花?
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花的朵数 | 1 | 2 | 3 | 4 | 5 | 6 |