题目内容
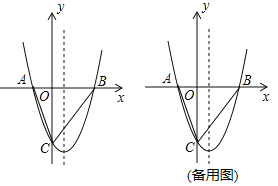
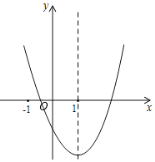
【题目】二次函数![]() 的图象如图所示,对称轴是直线
的图象如图所示,对称轴是直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数).其中结论正确的个数为( )
为实数).其中结论正确的个数为( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①由抛物线开口方向得到![]() ,对称轴在
,对称轴在![]() 轴右侧,得到
轴右侧,得到![]() 与
与![]() 异号,又抛物线与
异号,又抛物线与![]() 轴正半轴相交,得到
轴正半轴相交,得到![]() ,可得出
,可得出![]() ,选项①正确;
,选项①正确;
②把![]() 代入
代入![]() 中得
中得![]() ,所以②正确;
,所以②正确;
③由![]() 时对应的函数值
时对应的函数值![]() ,可得出
,可得出![]() ,得到
,得到![]() ,由
,由![]() ,
,![]() ,
,![]() ,得到
,得到![]() ,选项③正确;
,选项③正确;
④由对称轴为直线![]() ,即
,即![]() 时,
时,![]() 有最小值,可得结论,即可得到④正确.
有最小值,可得结论,即可得到④正确.
解:①∵抛物线开口向上,∴![]() ,
,
∵抛物线的对称轴在![]() 轴右侧,∴
轴右侧,∴![]() ,
,
∵抛物线与![]() 轴交于负半轴,
轴交于负半轴,
∴![]() ,
,
∴![]() ,①错误;
,①错误;
②当![]() 时,
时,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
把![]() 代入
代入![]() 中得
中得![]() ,所以②正确;
,所以②正确;
③当![]() 时,
时,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,所以③正确;
,所以③正确;
④∵抛物线的对称轴为直线![]() ,
,
∴![]() 时,函数的最小值为
时,函数的最小值为![]() ,
,
∴![]() ,
,
即![]() ,所以④正确.
,所以④正确.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】下表中给出了变量x与ax2,ax2+bx+c之间的部分对应值(表格中的符号“…”表示该项数据已经丢失)
x | -1 | 0 | 1 |
ax | … | … | 1 |
ax+ bx + c | 7 | 2 | … |
(1)写出这条抛物线的开口方向,顶点D的坐标;并说明它的变化情况;
(2)抛物线![]() 的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
(3)在(2)的条件下,设线段BD交x轴于点C,试写出∠BAD与∠DCO的数量关系,并说明理由.