题目内容
【题目】综合与探究
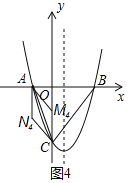
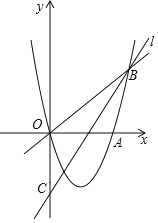
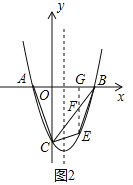
如图，抛物线y＝x2+bx+c与x轴交于A、B两点，与y轴交于C点，OA＝2，OC＝6，连接AC和BC．
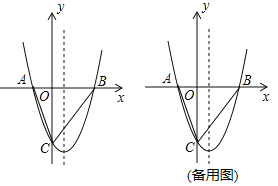
（1）求抛物线的解析式；
（2）点D在抛物线的对称轴上，当△ACD的周长最小时，点D的坐标为 ．
（3）点E是第四象限内抛物线上的动点，连接CE和BE．求△BCE面积的最大值及此时点E的坐标；
（4）若点M是y轴上的动点，在坐标平面内是否存在点N，使以点A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．
【答案】（1）y＝x2﹣x﹣6；（2）（
，﹣5）；（3）点E坐标为（
，﹣
）时，△BCE面积最大，最大值为
；（4）存在点N，点N坐标为（﹣2，2
），（﹣2，﹣2），（2，0），（﹣2，﹣
）．
【解析】
（1）用待定系数法求解；
（2）当点B、D、C在同一直线上时，C△ACD＝AC+AD+CD＝AC+BD+CD＝AC+BC最小；求出直线BC：y＝2x﹣6，可进一步求解；
（3）过点E作EG⊥x轴于点G，交直线BC与点F，设E（t，t2﹣t﹣6）（0＜t＜3），则F（t，2t﹣6），得EF＝2t﹣6﹣（t2﹣t﹣6）＝﹣t2+3t，S△BCE＝S△BEF+S△CEF＝﹣（t﹣）2+，可得结果；
（4）存在点N，使以点A、C、M、N为顶点的四边形是菱形．可分情况若AC为菱形的边长，MN∥AC且，MN＝AC＝2；若AC为菱形的对角线，则AN4∥CM4，AN4＝CN4，N4（﹣2，n），由勾股定理可求n.
（1）∵OA＝2，OC＝6
∴A（﹣2，0），C（0，﹣6）
∵抛物线y＝x2+bx+c过点A、C
∴
解得：
∴抛物线解析式为y＝x2﹣x﹣6
（2）∵当y＝0时，x2﹣x﹣6＝0，解得：x1＝﹣2，x2＝3
∴B（3，0），抛物线对称轴为直线x＝
∵点D在直线x＝上，点A、B关于直线x＝对称
∴xD＝，AD＝BD
∴当点B、D、C在同一直线上时，C△ACD＝AC+AD+CD＝AC+BD+CD＝AC+BC最小
设直线BC解析式为y＝kx﹣6
∴3k﹣6＝0，解得：k＝2
∴直线BC：y＝2x﹣6
∴yD＝2×﹣6＝﹣5
∴D（，﹣5）
故答案为：（，﹣5）
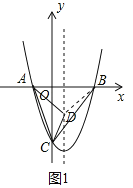
（3）过点E作EG⊥x轴于点G，交直线BC与点F
设E（t，t2﹣t﹣6）（0＜t＜3），则F（t，2t﹣6）
∴EF＝2t﹣6﹣（t2﹣t﹣6）＝﹣t2+3t
∴S△BCE＝S△BEF+S△CEF＝EFBG+EFOG＝EF（BG+OG）＝EFOB＝×3（﹣t2+3t）＝﹣（t﹣）2+
∴当t＝时，△BCE面积最大
∴yE＝（）2﹣﹣6＝﹣
∴点E坐标为（，﹣）时，△BCE面积最大，最大值为．
（4）存在点N，使以点A、C、M、N为顶点的四边形是菱形．
∵A（﹣2，0），C（0，﹣6）
∴AC＝
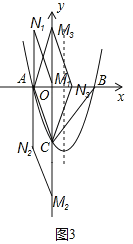
①若AC为菱形的边长，如图3，
则MN∥AC且，MN＝AC＝2
∴N1（﹣2，2），N2（﹣2，﹣2），N3（2，0）
②若AC为菱形的对角线，如图4，则AN4∥CM4，AN4＝CN4
设N4（﹣2，n）
∴﹣n＝
解得：n＝﹣
∴N4（﹣2，﹣）
综上所述，点N坐标为（﹣2，2），（﹣2，﹣2），（2，0），（﹣2，﹣）．
