题目内容
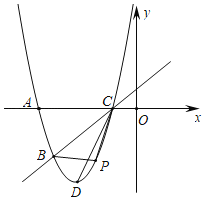
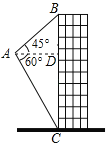
【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=∠ACB=90°,∠D=60°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对的直角边与Rt△ACB的斜边恰好重合.以AB为直径的圆经过点C,且与AD相交于点E,连接EB,连接CE并延长交BD于F.
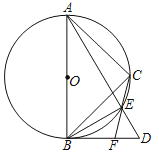
(1)求证:EF平分∠BED;
(2)求△BEF与△DEF的面积的比值.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用圆周角定理证明∠AEC=∠ABC=45°即可解决问题.
(2)首先证明BE=![]() DE,再利用三角形的面积公式计算即可.
DE,再利用三角形的面积公式计算即可.
(1)证明:∵CA=CB,∠ACB=90°,
∴∠ABC=∠AEC=45°,
∵AB是直径,
∴∠AEB=∠BED=90°,
∵∠AEC=∠DEF=45°,
∴FEB=∠FED=45°,
∴EF平分∠BED.
(2)解:∵∠BED=90°,∠D=60°,
∴tan∠D=![]() =
=![]() ,
,
∵S△BEF=![]() BEEFsin45°,S△EDF=
BEEFsin45°,S△EDF=![]() DEEFsin45°,
DEEFsin45°,
∴![]() =
=![]() =
=![]() .
.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目