题目内容
【题目】下表中给出了变量x与ax2,ax2+bx+c之间的部分对应值(表格中的符号“…”表示该项数据已经丢失)
x | -1 | 0 | 1 |
ax | … | … | 1 |
ax+ bx + c | 7 | 2 | … |
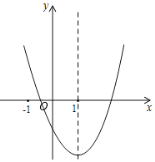
(1)写出这条抛物线的开口方向,顶点D的坐标;并说明它的变化情况;
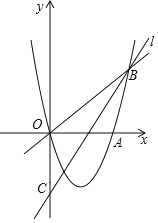
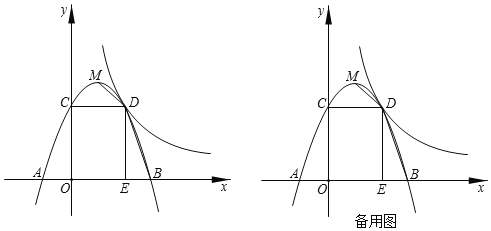
(2)抛物线![]() 的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
(3)在(2)的条件下,设线段BD交x轴于点C,试写出∠BAD与∠DCO的数量关系,并说明理由.
【答案】(1)![]() ,开口向上,
,开口向上,![]() ,变化情况见解析;(2)
,变化情况见解析;(2)![]() ;(3)
;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)根据(1,1)在抛物线y=ax2上可求出a值,再由(-1,7)、(0,2)在抛物线y=x2+bx+c上可求出b、c的值,即可得到答案;
(2)根据△ADM和△BDM同底可得出两三角形的面积比等于高的比,结合点A的坐标即可求出点B的横坐标,再利用二次函数图象上点的坐标特征即可求出点B的坐标;
(3)利用二次函数图象上点的坐标特征可求出A、D的坐标,过点A作AN∥x轴,交BD于点N,则∠AND=∠DCO,根据点B、D的坐标利用待定系数法可求出直线BD的解析式,利用一次函数图象上点的坐标特征可求出点N的坐标,利用两点间的距离公式可求出BA、BD、BN的长度,由三者间的关系结合∠ABD=∠NBA,可证出△ABD∽△NBA,根据相似三角形的性质可得出∠ANB=∠DAB,再由∠ANB+∠AND=180°可得出∠DAB+∠DCO=180°.
解:(1)当x=1时,y=ax2=1,
解得:a=1;
将(-1,7)、(0,2)代入y=x2+bx+c,得:
![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为![]() 或
或![]() ,
,
∴该抛物线的开口向上,顶点D(2,-2),
变化情况:在对称轴![]() 的左边y随x的增大而减小,再对称轴
的左边y随x的增大而减小,再对称轴![]() 的右边y随x的增大而增大;
的右边y随x的增大而增大;
(2)∵△ADM和△BDM同底,且△ADM与△BDM的面积比为2:3,
∴点A到抛物线的距离与点B到抛物线的距离比为2:3.
∵抛物线![]() 的对称轴为直线x=2,点A的横坐标为0,
的对称轴为直线x=2,点A的横坐标为0,
∴点B到抛物线对称轴的距离为3,
∴点B的横坐标为3+2=5,
∴点B的坐标为(5,7).
(3)∠BAD+∠DCO=180°,理由如下:
当x=0时,![]() ,
,
∴点A的坐标为(0,2),
∵![]()
![]() ,
,
∴点D的坐标为(2,-2).
过点A作AN∥x轴,交BD于点N,则∠AND=∠DCO,如图所示.
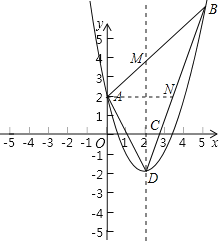
设直线BD的表达式为y=mx+n(m≠0),
将B(5,7)、D(2,-2)代入y=mx+n,
得到:![]() ,
,
解得:![]() ,
,
∴直线BD的表达式为y=3x-8.
当y=2时,有3x-8=2,
解得:![]() ,
,
∵A(0,2),B(5,7),D(2,-2),
∴![]() ,
,
∴![]() ,
,
又∵∠ABD=∠NBA,
∴△ABD∽△NBA,
∴∠ANB=∠DAB.
∵∠ANB+∠AND=180°,
∴∠DAB+∠DCO=180°.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案