题目内容
【题目】如图,抛物线y=ax2+bx+4与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,D为抛物线对称轴上一动点,求D运动到什么位置时△DAC的周长最小;
(3)如图2,点E在第一象限抛物线上,AE与BC交于点F,若AF:FE=2:1,求E点坐标;
(4)点M、N同时从B点出发,分别沿BA、BC方向运动,它们的运动速度都是1个单位/秒,当点M运动到点A时,点N停止运动,则当点N停止运动后,在x轴上是否存在点P,使得△PBN是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)点P的坐标P1(﹣1,0)或P2(7,0)或P3(﹣
(3)点P的坐标P1(﹣1,0)或P2(7,0)或P3(﹣![]() ,0)或P4(
,0)或P4(![]() ,0).
,0).
【解析】
(1)直接待定系数法代入求解即可 (2)找到D点在对称轴时是△DAC周长最小的点,先求出直线BC,然后D点横坐标是1,直接代入直线BC求出纵坐标即可 (3)作EH∥AB交BC于H,则∠FAB=∠FEH,∠FBA=∠FHE,易证△ABF∽△EHF,得![]() ,得EH=2,设E(x,
,得EH=2,设E(x,![]() ),则H(x﹣2,
),则H(x﹣2,![]() ),yE=yH,解出方程x=1或x=2,得到E点坐标 (4)△PBN是等腰三角形,分成三种情况,①BP=BC时,利用等腰三角性质直接得到P1(﹣1,0)或P2(7,0),②当NB=NP时,作NH⊥x轴,易得△NHB∽△COB,利用比例式得到NH、 BH从而得到 PH=BH,BP,进而得到OP,即得到P点坐标,③当PN=PB时,取NB中点K,作KP⊥BN,交x轴于点P,易得△NOB∽△PKB,利用比例式求出PB,进而得到OP,即求出P点坐标
),yE=yH,解出方程x=1或x=2,得到E点坐标 (4)△PBN是等腰三角形,分成三种情况,①BP=BC时,利用等腰三角性质直接得到P1(﹣1,0)或P2(7,0),②当NB=NP时,作NH⊥x轴,易得△NHB∽△COB,利用比例式得到NH、 BH从而得到 PH=BH,BP,进而得到OP,即得到P点坐标,③当PN=PB时,取NB中点K,作KP⊥BN,交x轴于点P,易得△NOB∽△PKB,利用比例式求出PB,进而得到OP,即求出P点坐标
解:(1)将A(﹣1,0)、B(3,0)代入y=ax2+bx+4,
得 ![]()
解得a=![]() ,b=
,b=![]() ,
,
∴抛物线的解析式![]() ;
;
(2)![]()
∴抛物线对称轴为直线x=1,
∴D的横坐标为1,
由(1)可得C(0,4),
∵B(3,0),
∴直线BC:![]()
∵DA=DB,
△DAC的周长=AC+CD+AD=AC+CD+BD,
连接BC,与对称轴交于点D,
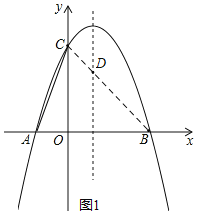
此时CD+BD最小,
∵AC为定值,
∴此时△DAC的周长,
当x=1时,y=﹣![]() ×1+4=
×1+4=![]() ,
,
∴D(1,![]() );
);
(3)作EH∥AB交BC于H,则∠FAB=∠FEH,∠FBA=∠FHE,

∴△ABF∽△EHF,
∵AF:FE=2:1,
∴![]() ,
,
∵AB=4,
∴EH=2,
设E(x,![]() ),则H(x﹣2,
),则H(x﹣2,![]() )
)
∵EH∥AB,
∴yE=yH,
∴![]() =
=![]()
解得x=1或x=2,
y=![]() 或4,
或4,
∴E(1,![]() )或(2,4);
)或(2,4);
(4)∵A(﹣1,0)、B(3,0),C(0,4)
∴AB=4,OC=4,
点M运动到点A时,BM=AB=4,
∴BN=4,
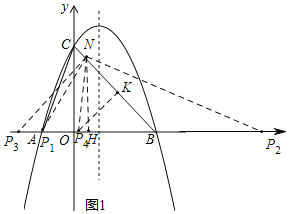
∵△PBN是等腰三角形,
①BP=BC时,
若P在点B左侧,OP=PB﹣OB=4﹣3=1,
∴P1(﹣1,0),
若P在点B右侧,OP=OB+BP=4+3=7,
∴P2(7,0);
②当NB=NP时,作NH⊥x轴,
△NHB∽△COB,
∴![]()
∴NH=![]() OC=
OC=![]() =
=![]() ,
,
BH=![]() BC=
BC=![]() ,
,
∴PH=BH=![]() ,
,
BP=![]() ,
,
∴OP=BP﹣OB=![]() ,
,
∴P3(﹣![]() ,0);
,0);
③当PN=PB时,
取NB中点K,作KP⊥BN,交x轴于点P,
∴△NOB∽△PKB,
∴![]()
∴PB=![]() ,
,
∴OP=OB﹣PB=3﹣![]() =
=![]()
P4(![]() ,0)
,0)
综上,当△PBN是等腰三角形时,点P的坐标P1(﹣1,0)或P2(7,0)或P3(﹣![]() ,0)或P4(
,0)或P4(![]() ,0).
,0).