Question

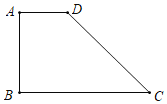
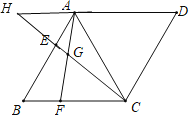
【题目】已知：如图，在菱形ABCD中，AB＝AC，点E、F分别在边AB、BC上，且AE＝BF，CE与AF相交于点G．

（1）求证：∠FGC＝∠B；

（2）延长CE与DA的延长线交于点H，求证：BECH＝AFAC．

Answer 1

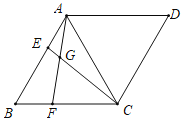
【答案】（1）见解析；（2）见解析.

【解析】

（1）先利用菱形的性质判断△ABC为等边三角形得到∠B＝∠BAC＝60°，再证明△ABF≌△CAE得到∠BAF＝∠ACE，然后利用角度代换可得到结论；

（2）如图，先证明△BCE∽△DHC得到，然后利用等线段代换可得到结论．

（1）∵四边形ABCD为菱形，

∴AB＝BC，

而AB＝AC，

∴AB＝BC＝AC，

∴△ABC为等边三角形，

∴∠B＝∠BAC＝60°，

在△ABF和△CAE中

，

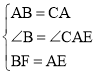∴△ABF≌△CAE（SAS），

∴∠BAF＝∠ACE，

∵∠FGC＝∠GAC+∠ACG＝∠GAC+∠BAF＝∠BAC＝60°，

∴∠FGC＝∠B；

（2）如图，

∵四边形ABCD为菱形，

∴∠B＝∠D，AD∥BC，

∴∠BCE＝∠H，

∴△BCE∽△DHC，

，

∵△ABF≌△CAE，

∴CE＝AF

∵CA＝CB＝CD，

∴，

∴BECH＝AFAC．