Question

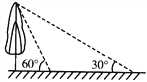
【题目】如图，一架无人机在距离地面高度为13.3米的点A处，测得地面点M的俯角为53°，这架无人机沿仰角为35°的方向飞行了55米到达点B，恰好在地面点N的正上方，M、N在同一水平线上求出M、N两点之间的距离．（结果精确到1米）

（参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33，sin35°≈0.57，cos35°≈0.82，tan35°≈0.70．）

Answer 1

【答案】35米

【解析】

过点A作AC⊥BN于C．过点M作MD⊥AC于D，在Rt△AMD中，通过解直角三角形可求出AD的长，在Rt△ABC中，通过解直角三角形可求出AC的长，由AC⊥BN，MD⊥AC，MN⊥BN可得出四边形MDCN是矩形，再利用矩形的性质即可求出MN的长，此题得解．

过点A作AC⊥BN于C．过点M作MD⊥AC于D，如图所示．

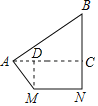
在Rt△AMD中，DM=13.3，∠DAM=53°，

∴AD10；

在Rt△ABC中，AB=55，∠BAC=35°，

∴AC=ABcos53°=55×0.82=45.1．

∵AC⊥BN，MD⊥AC，MN⊥BN，

∴四边形MDCN是矩形，

∴MN=DC=AC﹣AD≈35．

答：MN两点的距离约是35米．