ΧβΡΩΡΎ»ί
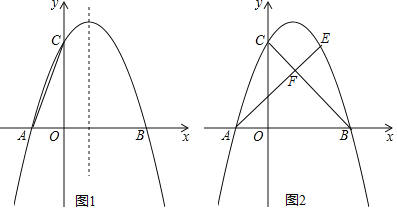
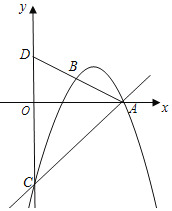
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ“―÷Σ≈ΉΈοœΏΨ≠Ιΐ‘≠ΒψOΚΆx÷α…œ“ΜΒψAΘ®4Θ§0Θ©Θ§≈ΉΈοœΏΕΞΒψΈΣEΘ§ΥϋΒΡΕ‘≥Τ÷α”κx÷αΫΜ”ΎΒψDΘ§÷±œΏy=©¹2x©¹1Ψ≠Ιΐ≈ΉΈοœΏ…œ“ΜΒψBΘ®©¹2Θ§mΘ©«“”κy÷αΫΜ”ΎΒψCΘ§”κ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΫΜ”ΎΒψFΘ°
Θ®1Θ©«σmΒΡ÷ΒΦΑΗΟ≈ΉΈοœΏΒΡΫβΈω Ϋ
Θ®2Θ©PΘ®xΘ§yΘ© «≈ΉΈοœΏ…œΒΡ“ΜΒψΘ§»τSΓςADP=SΓςADCΘ§«σ≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘ°
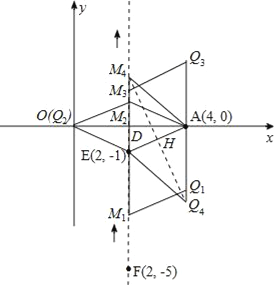
Θ®3Θ©ΒψQ «ΤΫΟφΡΎ»Έ“β“ΜΒψΘ§ΒψM¥”ΒψF≥ωΖΔΘ§―ΊΕ‘≥Τ÷αœρ…œ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·Θ§…ηΒψMΒΡ‘ΥΕ· ±ΦδΈΣtΟκΘ§ «ΖώΡή Ι“‘QΓΔAΓΔEΓΔMΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΩ»τΡήΘ§«κ÷±Ϋ”–¥≥ωΒψMΒΡ‘ΥΕ· ±ΦδtΒΡ÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ(1) 3 ![]() (2) P1Θ®2+2
(2) P1Θ®2+2![]() Θ§1Θ©P2=Θ®2©¹2
Θ§1Θ©P2=Θ®2©¹2![]() Θ§1Θ©Θ§P3Θ©2Θ§1Θ© (3) ¥φ‘Ύ
Θ§1Θ©Θ§P3Θ©2Θ§1Θ© (3) ¥φ‘Ύ
ΫβΘΚΘ®1Θ©ΓΏΒψBΘ®©¹2Θ§mΘ©‘Ύ÷±œΏy=©¹2x©¹1…œ
Γύm=©¹2ΓΝΘ®©¹2Θ©©¹1=4©¹1=3Θ§
Υυ“‘Θ§ΒψBΘ®©¹2Θ§3Θ©Θ§
”÷ΓΏ≈ΉΈοœΏΨ≠Ιΐ‘≠ΒψOΘ§
Γύ…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=ax2+bxΘ§
ΓΏΒψBΘ®©¹2Θ§3Θ©Θ§AΘ®4Θ§0Θ©‘Ύ≈ΉΈοœΏ…œΘ§
![]() Θ§
Θ§
ΫβΒΟ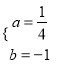 Θ°
Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΓΏPΘ®xΘ§yΘ© «≈ΉΈοœΏ…œΒΡ“ΜΒψΘ§
![]() Θ§
Θ§
»τSΓςADP=SΓςADCΘ§
![]() Θ§
Θ§ ![]() Θ§
Θ§
”÷ΓΏΒψC «÷±œΏy=©¹2x©¹1”κy÷αΫΜΒψΘ§
ΓύCΘ®0Θ§©¹1Θ©Θ§
ΓύOC=1Θ§
Γύ|![]() x2©¹x|=1Θ§Φ¥
x2©¹x|=1Θ§Φ¥![]() x2©¹x=1Θ§Μρ
x2©¹x=1Θ§Μρ![]() x2©¹x=©¹1Θ§
x2©¹x=©¹1Θ§
ΫβΒΟΘΚx1=2+2![]() Θ§x2=2©¹2
Θ§x2=2©¹2![]() Θ§x3=x4=2Θ§
Θ§x3=x4=2Θ§
ΓύΒψPΒΡΉχ±ξΈΣ P1Θ®2+2![]() Θ§1Θ©P2=Θ®2©¹2
Θ§1Θ©P2=Θ®2©¹2![]() Θ§1Θ©Θ§P3Θ©2Θ§1Θ©ΘΜ
Θ§1Θ©Θ§P3Θ©2Θ§1Θ©ΘΜ
Θ®3Θ©Ϋα¬έΘΚ¥φ‘ΎΘ°
ΓΏ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=![]() x2©¹xΘ§
x2©¹xΘ§
ΓύΕΞΒψEΘ®2Θ§©¹1Θ©Θ§Ε‘≥Τ÷αΈΣx=2ΘΜ
ΒψF «÷±œΏy=©¹2x©¹1”κΕ‘≥Τ÷αx=2ΒΡΫΜΒψΘ§ΓύFΘ®2Θ§©¹5Θ©Θ§DF=5Θ°
”÷ΓΏAΘ®4Θ§0Θ©Θ§
ΓύAE=![]() Θ°
Θ°
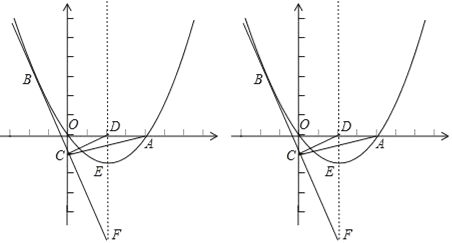
»γ”“ΆΦΥυ ΨΘ§‘ΎΒψMΒΡ‘ΥΕ·Ιΐ≥Χ÷–Θ§“ά¥Έ≥ωœ÷ΥΡΗωΝβ–ΈΘΚ
ΔΌΝβ–ΈAEM1Q1Θ°
ΓΏ¥Υ ±EM1=AE=![]() Θ§
Θ§
ΓύM1F=DF©¹DE©¹DM1=4©¹![]() Θ§
Θ§
Γύt1=4©¹![]() ΘΜ
ΘΜ
ΔΎΝβ–ΈAEOM2Θ°
ΓΏ¥Υ ±DM2=DE=1Θ§
ΓύM2F=DF+DM2=6Θ§
Γύt2=6ΘΜ
ΔέΝβ–ΈAEM3Q3Θ°
ΓΏ¥Υ ±EM3=AE=![]() Θ§
Θ§
ΓύDM3=EM3©¹DE=![]() ©¹1Θ§
©¹1Θ§
ΓύM3F=DM3+DF=Θ®![]() ©¹1Θ©+5=4+
©¹1Θ©+5=4+![]() Θ§
Θ§
Γύt3=4+![]() ΘΜ
ΘΜ
ΔήΝβ–ΈAM4EQ4Θ°
¥Υ ±AEΈΣΝβ–ΈΒΡΕ‘Ϋ«œΏΘ§…ηΕ‘Ϋ«œΏAE”κM4Q4ΫΜ”ΎΒψHΘ§‘ρAEΓΆM4Q4Θ§
ΓΏ“Ή÷ΣΓςAEDΓΉΓςM4EHΘ§
![]() Θ§Φ¥
Θ§Φ¥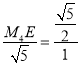 Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
ΓύDM4=M4E©¹DE=![]() ©¹1=
©¹1=![]() Θ§
Θ§
ΓύM4F=DM4+DF=![]() +5=
+5=![]() Θ§
Θ§
Γύt4=![]() Θ°
Θ°
Ήέ…œΥυ ωΘ§¥φ‘ΎΒψMΓΔΒψQΘ§ ΙΒΟ“‘QΓΔAΓΔEΓΔMΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΜ ±ΦδtΒΡ÷ΒΈΣΘΚt1=4©¹![]() Θ§t2=6Θ§t3=4+
Θ§t2=6Θ§t3=4+![]() Θ§t4=
Θ§t4=![]() Θ°
Θ°
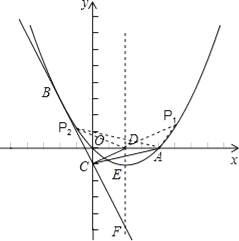
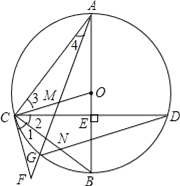
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΫΪx=-2¥ζ»κy=-2x-1Φ¥Ω…«σΒΟΒψBΒΡΉχ±ξΘ§ΗυΨί≈ΉΈοœΏΙΐΒψAΓΔOΓΔBΦ¥Ω…«σ≥ω≈ΉΈοœΏΒΡΖΫ≥Χ.
Θ®2Θ©ΗυΨίΧβ“βΘ§Ω…÷ΣΓςADPΚΆΓςADCΒΡΗΏœύΒ»Θ§Φ¥ΒψPΉίΉχ±ξΒΡΨχΕ‘÷ΒΈΣ1Θ§Υυ“‘ΒψPΒΡΉίΉχ±ξΈΣ![]() Θ§Ζ÷±π¥ζ»κ
Θ§Ζ÷±π¥ζ»κ![]() ÷–«σΫβΘ§Φ¥Ω…ΒΟΒΫΥυ”–ΖϊΚœΧβ“βΒΡΒψPΒΡΉχ±ξΓΘ
÷–«σΫβΘ§Φ¥Ω…ΒΟΒΫΥυ”–ΖϊΚœΧβ“βΒΡΒψPΒΡΉχ±ξΓΘ
Θ®3Θ©”…≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() Θ§ΒΟΕΞΒψEΘ®2Θ§©¹1Θ©Θ§Ε‘≥Τ÷αΈΣx=2ΘΜ
Θ§ΒΟΕΞΒψEΘ®2Θ§©¹1Θ©Θ§Ε‘≥Τ÷αΈΣx=2ΘΜ
ΒψF «÷±œΏy=©¹2x©¹1”κΕ‘≥Τ÷αx=2ΒΡΫΜΒψΘ§«σ≥ωFΘ®2Θ§©¹5Θ©Θ§DF=5Θ°
”÷”…AΘ®4Θ§0Θ©Θ§ΗυΨίΙ¥Ι…Ε®άμΒΟ![]() Θ°»ΜΚσΖ÷4÷÷«ιΩω«σΫβ.
Θ°»ΜΚσΖ÷4÷÷«ιΩω«σΫβ.

 100Ζ÷¥≥ΙΊΤΎΡ©≥ε¥ΧœΒΝ–¥πΑΗ
100Ζ÷¥≥ΙΊΤΎΡ©≥ε¥ΧœΒΝ–¥πΑΗ