题目内容
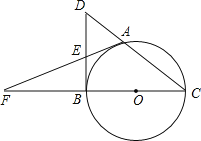
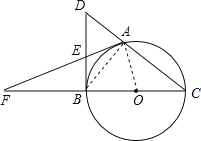
【题目】如图,A是以BC为直径的⊙O上一点,过点B作⊙O的切线,与CA的延长线相交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.
(1)求证:AF是⊙O的切线;
(2)若BE=5,BF=12,求CD的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用直角三角形斜边中线的性质和等边对等角得到∠EAB=∠EBA,结合⊙O的切线得出OA⊥AF,从而得出AF是⊙O的切线;
(2)先根据勾股定理求得EF的长,再根据切线的性质得出EB=EA=5,即可求得AF的长,然后根据切割线定理求得FC,进而得出BC的长,根据E是BD的中点,得出BD的长,最后根据勾股定理即可求得CD的长.
解:(1)连接AB,OA,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵DB是⊙O的切线,
∴DB⊥BC,
∴∠DBO=90°,
在RT△ABD中,E是斜边BD的中线,
∴AE=DE=BE,
∴∠EAB=∠EBA,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠EAB+∠OAB=∠EBA+∠OBA
∴∠EAO=∠DBO=90°,
∴OA⊥AF,
∴AF是⊙O的切线;
(2)∵在RT△BEF中,BE=5,BF=12,
∴EF=![]() =13,
=13,
∵FA、DB是⊙O的切线,
∴EA=EB=5,
∴AF=EF+EA=13+5=18,
∵AF2=FBFC,
∴FC=![]()
∴BC=FC﹣FB=27﹣12=15,
∵E是BD的中点,
∴BD=2BE=10,
在RT△DBC中,![]() .
.

【题目】郑州市创建国家生态园林城市实施方案已经出台,到2019年5月底,市区主城区要达到或超过《国家生态园林城市标准》各项指标要求.郑州市林荫路推广率要超过85%,在推进此活动中,郑州市某小区决定购买A、B两种乔木树,经过调查,获取信息如下:如果购买A种树木40棵,B种树木60棵,需付款11400元;如果购买A种树木50棵,B种树木50棵,需付款10500元.
树种 | 购买数量低于50棵 | 购买数量不低于50棵 |
A | 原价销售 | 以八折销售 |
B | 原价销售 | 以九折销售 |
(1)A种树木与B种树木的单价各多少元?
(2)经过测算,需要购置A、B两种树木共100棵,其中B种树木的数量不多于A种树木的三分之一,如何购买付款最少?最少费用是多少元?请说明理由.